题目内容
操作与探索:
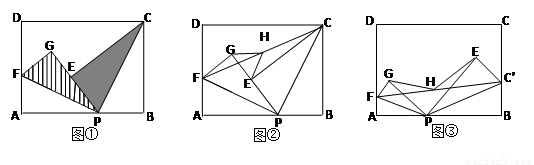
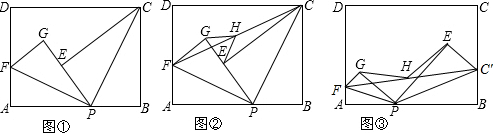
已知点O为直线AB上一点,作射线OC,将直角三角板ODE放置在直线上方(如图①),使直角顶点与点O重合,一条直角边OD重叠在射线OA上,将三角板绕点O旋转
(1)当三角板旋转到如图②的位置时,若OD平分∠AOC,试说明OE也平分∠BOC.
(2)若OC⊥AB,垂足为点O(如图③),请直接写出与∠DOB互补的角
(3)若∠AOC=135°(如图④),三角板绕点O按顺时针从如图①的位置开始旋转,到OE边与射线OB重合结束. 请通过操作,探索:在旋转过程中,∠DOB ∠COE的差是否发生变化?若不变,请求出这个差值;若变化,请用含有n(n为三角板旋转的度数)的代数式表示这个差.
∠COE的差是否发生变化?若不变,请求出这个差值;若变化,请用含有n(n为三角板旋转的度数)的代数式表示这个差.
(1)由OD平分∠AOC可得∠AOD=∠COD,由∠DOE=90°可得∠AOD+∠EOB=90°,∠COD+∠COE=90°,即可证得结论;(2)∠AOD、∠COE;
(3)①若n≤45°,∠DOB ∠COE=135°,②若n>45°,∠DOB
∠COE=135°,②若n>45°,∠DOB ∠COE=225°
∠COE=225° 2n
2n
解析试题分析:(1)由OD平分∠AOC可得∠AOD=∠COD,由∠DOE=90°可得∠AOD+∠EOB=90°,∠COD+∠COE=90°,即可证得结论;
(2)由OC⊥AB可得∠AOD+∠COD=90°,由∠DOE=90°可得∠COD+∠COE=90°,即可得到∠AOD=∠COE,从而可以求得与∠DOB互补的角;
(3)由于旋转45°时,OE与OC重合,故要分n≤45°与n>45°两种情况分析.
(1)∵OD平分∠AOC
∴∠AOD=∠COD
∵∠DOE=90°
∴∠AOD+∠EOB=90°,∠COD+∠COE=90°
∴∠COE=∠EOB
∴OE也平分∠BOC;
(2)∵OC⊥AB,∠DOE=90°
∴∠AOD+∠COD=90°,∠COD+∠COE=90°
∴∠AOD=∠COE
∴与∠DOB互补的角为∠AOD、∠COE;
(3)①若n≤45°,∠DOB ∠COE=(180°-n)-(45°-n)=180°-n-45°+n=135°,
∠COE=(180°-n)-(45°-n)=180°-n-45°+n=135°,
②若n>45°,∠DOB ∠COE=(180°-n)-(n-45°)=180°-n-n+45°=225°
∠COE=(180°-n)-(n-45°)=180°-n-n+45°=225° 2n.
2n.
考点:旋转的性质,角平分线的性质,互补的定义,同角的余角相等
点评:解答本题的关键是注意直角三角板的问题往往应用到同角的余角相等的知识,同时熟记旋转对应边是夹角是旋转角.

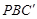 沿
沿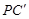 翻折得到△
翻折得到△ ,连接
,连接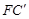 ,取
,取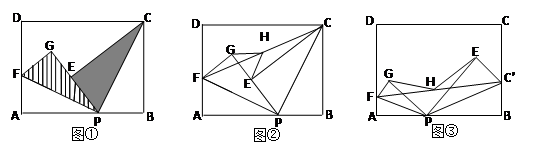

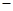 ∠COE的差是否发生变化?若不变,请求出这个差值;若变化,请用含有n(n为三角板旋转的度数)的代数式表示这个差.
∠COE的差是否发生变化?若不变,请求出这个差值;若变化,请用含有n(n为三角板旋转的度数)的代数式表示这个差.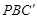 沿
沿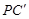 翻折得到△
翻折得到△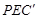 ,连接
,连接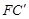 ,取
,取