摘要:函数:的自变量的取值范围是 ( ) A.≤ B.≥ C.≥ D.≤
网址:http://m.1010jiajiao.com/timu3_id_456964[举报]
给出函数y=x+
.
(1)写出自变量x的取值范围;
(2)请通过列表、描点、连线画出这个函数的图象;
①列表:
②描点(在下面给出的直角坐标中描出上表对应的各点):

③连线(将上图中描出的各点用平滑曲线连接起来,得到函数图象)
(3)观察函数图象,回答下列问题:
①函数图象在第 象限;
②函数图象的对称性是( )
A.既是轴对称图形,又是中心对称图形
B.只是轴对称图形,不是中心对称图形
C.不是轴对称图形,而是中心对称图形
D.既不是轴对称图形,也不是中心对称图形
③在x>0时,当x= 时,函数y有最 (大,小)值,且这个最值等于 ;
在x<0时,当x= 时,函数y有最 (大,小)值,且这个最值等于 ;
④在第一象限内,x在什么范围内,y随着x增大而减小,x在什么范围内,y随x增
大而增大;
(4)方程x+
=-2x+1是否有实数解?说明理由.
查看习题详情和答案>>
| 1 |
| x |
(1)写出自变量x的取值范围;
(2)请通过列表、描点、连线画出这个函数的图象;
①列表:
| x | … | -4 | -3 | -2 | -1 | -
|
-
|
-
|
|
|
|
1 | 2 | 3 | 4 | … | ||||||||||||
| y | … | … |

③连线(将上图中描出的各点用平滑曲线连接起来,得到函数图象)
(3)观察函数图象,回答下列问题:
①函数图象在第
②函数图象的对称性是(
A.既是轴对称图形,又是中心对称图形
B.只是轴对称图形,不是中心对称图形
C.不是轴对称图形,而是中心对称图形
D.既不是轴对称图形,也不是中心对称图形
③在x>0时,当x=
在x<0时,当x=
④在第一象限内,x在什么范围内,y随着x增大而减小,x在什么范围内,y随x增
大而增大;
(4)方程x+
| 1 |
| x |
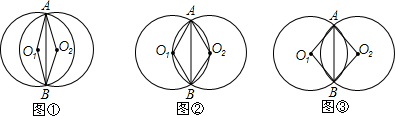
如图①、②、③是两个半径都等于2的⊙O1和⊙O2,由重合状态沿水平方向运动到互相外切过程中的三个位置,⊙O1和⊙O2相交于A、B两点,分别连接O1A、O1B、O2A、O2B和AB.
(1)如图②,当∠AO1B=120°时,求两圆重叠部分图形的周长l;
(2)设∠AO1B的度数为x,两圆重叠部分图形的周长为y,求y关于x的函数关系式,并写出自变量x的取值范围;
(3)由(2),若y=2π,则线段O2A所在的直线与⊙O1有何位置关系,为什么?除此之外,它们还有其它的位置关系,写出其它位置关系时x的取值范围.(奖励提示:如果你还能解决下列问题,将酌情另加1~5分,并计入总分.)
在原题的条件下,设∠AO1B的度数为2n,可以发现有些图形的面积S也随∠AO1B变化而变化,试求出其中一个S与n的关系式,并写出n的取值范围.
 查看习题详情和答案>>
查看习题详情和答案>>
(1)如图②,当∠AO1B=120°时,求两圆重叠部分图形的周长l;
(2)设∠AO1B的度数为x,两圆重叠部分图形的周长为y,求y关于x的函数关系式,并写出自变量x的取值范围;
(3)由(2),若y=2π,则线段O2A所在的直线与⊙O1有何位置关系,为什么?除此之外,它们还有其它的位置关系,写出其它位置关系时x的取值范围.(奖励提示:如果你还能解决下列问题,将酌情另加1~5分,并计入总分.)
在原题的条件下,设∠AO1B的度数为2n,可以发现有些图形的面积S也随∠AO1B变化而变化,试求出其中一个S与n的关系式,并写出n的取值范围.
 查看习题详情和答案>>
查看习题详情和答案>>
二次函数y=ax2+bx+c的自变量x与函数值y的部分对应值如下表:
根据表格中的信息,完成下列各题
(1)当x=3时,y= ;
(2)当x= 时,y有最 值为 ;
(3)若点A(x1,y1)、B(x2,y2)是该二次函数图象上的两点,且-1<x1<0,1<x2<2,试比较两函数值的大小:y1 y2
(4)若自变量x的取值范围是0≤x≤5,则函数值y的取值范围是 .
查看习题详情和答案>>
| x | … | -1 | 0 | 1 | 2 | 3 | … | ||||
| y | … | -1 | -
|
-2 | -
|
… |
(1)当x=3时,y=
(2)当x=
(3)若点A(x1,y1)、B(x2,y2)是该二次函数图象上的两点,且-1<x1<0,1<x2<2,试比较两函数值的大小:y1
(4)若自变量x的取值范围是0≤x≤5,则函数值y的取值范围是