题目内容
二次函数y=ax2+bx+c的自变量x与函数值y的部分对应值如下表:| x | … | -1 | 0 | 1 | 2 | 3 | … | ||||
| y | … | -1 | -
|
-2 | -
|
… |
(1)当x=3时,y=
(2)当x=
(3)若点A(x1,y1)、B(x2,y2)是该二次函数图象上的两点,且-1<x1<0,1<x2<2,试比较两函数值的大小:y1
(4)若自变量x的取值范围是0≤x≤5,则函数值y的取值范围是
分析:(1)由表中给出的三组数据,列方程组求得二次函数的解析式,再求出x=3时,y的值;
(2)实际上是求二次函数的顶点坐标;
(3)求得抛物线与x轴的两个交点坐标,在对称轴的左侧,y随x的增大而减小;在对称轴的右侧,y随x的增大而增大;再进行判断即可;
(4)根据抛物线的顶点,当x=5时,y最大,当x=1时,y最小.
(2)实际上是求二次函数的顶点坐标;
(3)求得抛物线与x轴的两个交点坐标,在对称轴的左侧,y随x的增大而减小;在对称轴的右侧,y随x的增大而增大;再进行判断即可;
(4)根据抛物线的顶点,当x=5时,y最大,当x=1时,y最小.
解答:解:(1)由表得
,解得
,∴二次函数的解析式为y=
x2-
x-
,
当x=3时,y=
×9 -
× 3-
=-1;
(2)将y=
x2-
x-
配方得,y=
(x-1)2-2,
∵a=
>0,∴函数有最小值,当x=1时,最小值为-2;
(3)令y=0,则x=±2
+1,抛物线与x轴的两个交点坐标为(2
+1,0)(-2
+1,0)
∵-1<x1<0,1<x2<2,∴x1到1的距离大于x2到1的距离,∴y1>y2
(4)∵抛物线的顶点为(1,-2),∴当x=5时,y最大,即y=2;当x=1时,y最小,即y=-2,
∴函数值y的取值范围是-2≤y≤2;
故答案为-1;1、小、-2;>;-2≤y≤2.
|
|
| 1 |
| 4 |
| 1 |
| 2 |
| 7 |
| 4 |
当x=3时,y=
| 1 |
| 4 |
| 1 |
| 2 |
| 7 |
| 4 |
(2)将y=
| 1 |
| 4 |
| 1 |
| 2 |
| 7 |
| 4 |
| 1 |
| 4 |
∵a=
| 1 |
| 4 |
(3)令y=0,则x=±2
| 2 |
| 2 |
| 2 |
∵-1<x1<0,1<x2<2,∴x1到1的距离大于x2到1的距离,∴y1>y2
(4)∵抛物线的顶点为(1,-2),∴当x=5时,y最大,即y=2;当x=1时,y最小,即y=-2,
∴函数值y的取值范围是-2≤y≤2;
故答案为-1;1、小、-2;>;-2≤y≤2.
点评:本题考查了用图象法求一元二次方程的近似根,是中考压轴题,难度较大.

练习册系列答案
 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案
相关题目
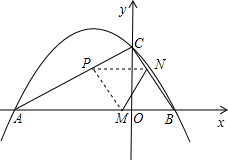 点C
点C 如图为二次函数y=ax2+bx+c(a≠0)的图象,则下列说法:①abc>0;②2a+b=0;③a+b+c>0;④当-1<x<3时,y>0.其中正确结论的序号是
如图为二次函数y=ax2+bx+c(a≠0)的图象,则下列说法:①abc>0;②2a+b=0;③a+b+c>0;④当-1<x<3时,y>0.其中正确结论的序号是 (2012•孝感)二次函数y=ax2+bx+c(a,b,c是常数,a≠0)图象的对称轴是直线x=1,其图象的一部分如图所示.对于下列说法:
(2012•孝感)二次函数y=ax2+bx+c(a,b,c是常数,a≠0)图象的对称轴是直线x=1,其图象的一部分如图所示.对于下列说法: