摘要:方法1:直接利用直角的刻度线或者三角板的直角来画. 方法2:尺规作图 (1)过直线上一点作一条直线与已知直线垂直 如图.点A在上.过点A作直线.使得⊥ 作法:1.以点A为圆心.以为适当长为半径画弧交于B.C
网址:http://m.1010jiajiao.com/timu3_id_456717[举报]
一副直角三角板由一块含30°的直角三角板与一块等腰直角三角板组成,且含30°角的三角板的较长直角边与另一三角板的斜边相等(如图1)
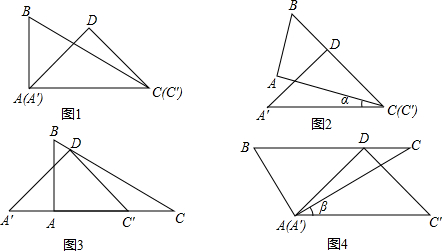
(1)如图1,这副三角板中,已知AB=2,AC=
(2)这副三角板如图1放置,将△A′DC′固定不动,将△ABC通过旋转或者平移变换可使△ABC的斜边BC经过△A′DC′′的直角顶点D.
方法一:如图2,将△ABC绕点C按顺时针方向旋转角度α(0°<α<180°)
方法二:如图3,将△ABC沿射线A′C′方向平移m个单位长度
方法三:如图4,将△ABC绕点A按逆时针方向旋转角度β(0°<β<180°)
请你解决下列问题:
①根据方法一,直接写出α的值为:
②根据方法二,计算m的值;
③根据方法三,求β的值.
(3)若将△ABC从图1位置开始沿射线A′C′平移,设AA′=x,两三角形重叠部分的面积为y,请直接写出y与x之间的函数关系式和相应的自变量x的取值范围.
查看习题详情和答案>>

(1)如图1,这副三角板中,已知AB=2,AC=
2
| 3 |
2
,A′D=| 3 |
| 6 |
| 6 |
(2)这副三角板如图1放置,将△A′DC′固定不动,将△ABC通过旋转或者平移变换可使△ABC的斜边BC经过△A′DC′′的直角顶点D.
方法一:如图2,将△ABC绕点C按顺时针方向旋转角度α(0°<α<180°)
方法二:如图3,将△ABC沿射线A′C′方向平移m个单位长度
方法三:如图4,将△ABC绕点A按逆时针方向旋转角度β(0°<β<180°)
请你解决下列问题:
①根据方法一,直接写出α的值为:
15°
15°
;②根据方法二,计算m的值;
③根据方法三,求β的值.
(3)若将△ABC从图1位置开始沿射线A′C′平移,设AA′=x,两三角形重叠部分的面积为y,请直接写出y与x之间的函数关系式和相应的自变量x的取值范围.
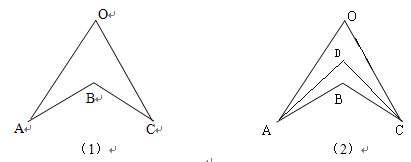
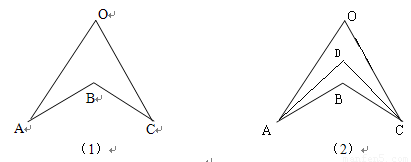
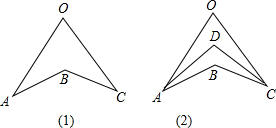
如图(1),由三角形的内角和或外角和可知:∠ABC=∠A+∠C+∠O在图(2)中,直接利用上述的结论探究:
①若AD、CD分别平分∠OAB,∠OCB,且∠O=80°∠B=120°,求∠ADC的度数
②AD、CD分别平分∠OAB,∠OCB,猜想∠O,∠ABC,∠ADC之间的等量关系,并说明理由.
查看习题详情和答案>>
①若AD、CD分别平分∠OAB,∠OCB,且∠O=80°∠B=120°,求∠ADC的度数
②AD、CD分别平分∠OAB,∠OCB,猜想∠O,∠ABC,∠ADC之间的等量关系,并说明理由.

计算下列各式:
(1)1-
= ;
(2)(1-
)(1-
)= ;
(3)(1-
)(1-
)(1-
)= ;
你能根据所学知识找到计算上面算式的简便方法吗?请利用找到的简便方法计算下式:(1-
)(1-
)(1-
)…(1-
).
查看习题详情和答案>>
(1)1-
| 1 |
| 22 |
(2)(1-
| 1 |
| 22 |
| 1 |
| 32 |
(3)(1-
| 1 |
| 22 |
| 1 |
| 32 |
| 1 |
| 42 |
你能根据所学知识找到计算上面算式的简便方法吗?请利用找到的简便方法计算下式:(1-
| 1 |
| 22 |
| 1 |
| 32 |
| 1 |
| 42 |
| 1 |
| 20112 |