摘要：例1.已知知线段a和b.如下图.求作一线段.使它的长度等于a+b. a b 作法:1.作 OA
网址：http://m.1010jiajiao.com/timu3_id_456699[举报]
如图，以△ABC的边AB、AC为直角边向外作等腰直角△ABE和△ACD，M是BC的中点，请你探究线段DE与AM之间的关系．
说明：（1）如果你经历反复探索，没有找到解决问题的方法，请你把探索过程中的某种思路写出来（要求至少写3步）；
（2）在你经历说明（1）的过程之后，可以从下列①、②中选取一个补充或更换已知条件，完成你的证明．
①画出将△ACM绕某一点顺时针旋转180°后的图形；
②∠BAC=90°（如图）
附加题：如图，若以△ABC的边AB、AC为直角边，向内作等腰直角△ABE和△ACD，其它条件不变，试探究线段DE与AM之间的关系．
查看习题详情和答案>>
说明：（1）如果你经历反复探索，没有找到解决问题的方法，请你把探索过程中的某种思路写出来（要求至少写3步）；
（2）在你经历说明（1）的过程之后，可以从下列①、②中选取一个补充或更换已知条件，完成你的证明．
①画出将△ACM绕某一点顺时针旋转180°后的图形；
②∠BAC=90°（如图）
附加题：如图，若以△ABC的边AB、AC为直角边，向内作等腰直角△ABE和△ACD，其它条件不变，试探究线段DE与AM之间的关系．
查看习题详情和答案>>
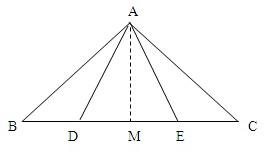21、如图，已知点B、D、E、C在同一直线上，AB=AC，AD=AE．求证：BD=CE
（1）根据下面说理步骤填空
证法一：作AM⊥BC，垂足为M．
∵AB=AC（
已知
） AM⊥BC（ 辅助线 ）∴BM=CM（
三线合一
）同理DM=EM．
∴BM-DM=CM-EM（
等量代换
）∴BD=CE（线段和、差的意义）
（2）根据下面证法二的辅助线完成后面的说理步骤．
证法二：作△ABC的中线AM．
如图，Rt△ABO的两直角边OA、OB分别在x轴的负半轴和y轴的正半轴上，O为坐标原点，A、B两点的坐标分别为（-3，0）、（0，4），抛物线
经过B点，且顶点在直线
上．
1.求抛物线对应的函数关系式；
2.若△DCE是由△ABO沿x轴向右平移得到的，当四边形ABCD是菱形时，试判断点C和点D是否在该抛物线上，并说明理由
3.在（2）的条件下，连结BD，已知在对称轴上存在一点P，使得△PBD的周长最小．请求出点P的坐标．
4.在（2）、（3）的条件下，若点M是线段OB上的一个动点（与点O、B不重合），过点M作MN∥BD交x轴于点N，连结PM、PN，设OM的长为t，△PMN的面积为S，求S与t的函数关系式，并写出自变量t的取值范围．S是否存在最大值？若存在，求出最大值并求此时M点的坐标；若不存在，请说明理由．
查看习题详情和答案>>
如图，Rt△ABO的两直角边OA、OB分别在x轴的负半轴和y轴的正半轴上，O为坐标原点，A、B两点的坐标分别为（-3，0）、（0，4），抛物线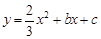
经过B点，且顶点在直线
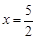上．
【小题1】求抛物线对应的函数关系式；
【小题2】若△DCE是由△ABO沿x轴向右平移得到的，当四边形ABCD是菱形时，试判断点C和点D是否在该抛物线上，并说明理由
【小题3】在（2）的条件下，连结BD，已知在对称轴上存在一点P，使得△PBD的周长最小．请求出点P的坐标．
【小题4】在（2）、（3）的条件下，若点M是线段OB上的一个动点（与点O、B不重合），过点M作MN∥BD交x轴于点N，连结PM、PN，设OM的长为t，△PMN的面积为S，求S与t的函数关系式，并写出自变量t的取值范围．S是否存在最大值？若存在，求出最大值并求此时M点的坐标；若不存在，请说明理由． 查看习题详情和答案>>
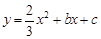经过B点，且顶点在直线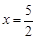上．【小题1】求抛物线对应的函数关系式；
【小题2】若△DCE是由△ABO沿x轴向右平移得到的，当四边形ABCD是菱形时，试判断点C和点D是否在该抛物线上，并说明理由
【小题3】在（2）的条件下，连结BD，已知在对称轴上存在一点P，使得△PBD的周长最小．请求出点P的坐标．
【小题4】在（2）、（3）的条件下，若点M是线段OB上的一个动点（与点O、B不重合），过点M作MN∥BD交x轴于点N，连结PM、PN，设OM的长为t，△PMN的面积为S，求S与t的函数关系式，并写出自变量t的取值范围．S是否存在最大值？若存在，求出最大值并求此时M点的坐标；若不存在，请说明理由． 查看习题详情和答案>>