摘要：图1是边长分别为4和3的两个等边三角形纸片ABC和C′D′E′叠放在一起(C与C′重合). (1)操作:固定△ABC.将△C′D′E′绕点C顺时针旋转30°得到△CDE.连结AD.BE.CE的延长线交AB于F(图2), 探究:在图2中.线段BE与AD之间有怎样的大小关系?试证明你的结论. (2)操作:将图2中的△CDE.在线段CF上沿着CF方向以每秒1个单位的速度平移.平移后的△CDE设为△PQR(图3), 探究:设△PQR移动的时间为x秒.△PQR与△ABC重叠部分的面积为y.求y与x之间的函数解析式.并写出函数自变量x的取值范围. (3)操作:图1中△C′D′E′固定.将△ABC移动.使顶点C落在C′E′的中点.边BC交D′E′于点M.边AC交D′C′于点N.设∠AC C′=α(30°＜α＜90°＝(图4), 探究:在图4中.线段C′N·E′M的值是否随α的变化而变化?如果没有变化.请你求出C′N·E′M的值.如果有变化.请你说明理由.
网址：http://m.1010jiajiao.com/timu3_id_456496[举报]
图1是边长分别为4
和3的两个等边三角形纸片ABC和C′D′E′叠放在一起（C与C′重合）．
（1）操作：固定△ABC，将△C′D′E′绕点C顺时针旋转30°得到△CDE，连接AD，BE，CE的延长线交AB于F（图2）．
探究：在图2中，线段BE与AD之间有怎样的大小关系？试证明你的结论；
（2）操作：将图2中的△CDE，在线段CF上沿着CF方向以每秒1个单位的速度平移，平移后的△CDE设为△PQR（图3）．
探究：设△PQR移动的时间为x秒，△PQR与△AFC重叠部分的面积为y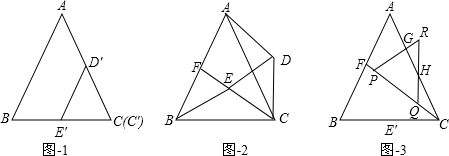
，求y与x之间的函数解析式，并写出函数自变量x的取值范围．
查看习题详情和答案>>
| 3 |
（1）操作：固定△ABC，将△C′D′E′绕点C顺时针旋转30°得到△CDE，连接AD，BE，CE的延长线交AB于F（图2）．
探究：在图2中，线段BE与AD之间有怎样的大小关系？试证明你的结论；
（2）操作：将图2中的△CDE，在线段CF上沿着CF方向以每秒1个单位的速度平移，平移后的△CDE设为△PQR（图3）．
探究：设△PQR移动的时间为x秒，△PQR与△AFC重叠部分的面积为y
，求y与x之间的函数解析式，并写出函数自变量x的取值范围．
查看习题详情和答案>>
图1是边长分别为4
和3的两个等边三角形纸片ABC和C′D′E′叠放在一起（C与C′重合）．
（1）操作：固定△ABC，将△C′D′E′绕点C顺时针旋转30°得到△CDE，连接AD、BE，CE的延长线交AB于F（图2）；
探究：在图2中，线段BE与AD之间有怎样的大小关系？试证明你的结论．
（2）操作：将图2中的△CDE，在线段CF上沿着CF方向以每秒1个单位的速度平移，平移后的△CDE设为△PQR（图3）；
请问：经过多少时间，△PQR与△ABC重叠部分的面积恰好等于
？
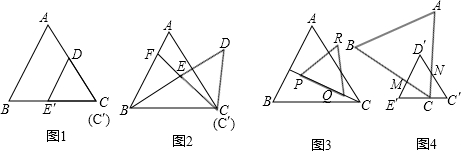
（3）操作：图1中△C′D′E′固定，将△ABC移动，使顶点C落在C′E′的中点，边BC交D′E′于点M，边AC交D′C′于点N，设
∠AC C′=α（30°＜α＜90，图4）；
探究：在图4中，线段C′N•E′M的值是否随α的变化而变化？如果没有变化，请你求出C′N•E′M的值，如果有变化，请你说明理由．
查看习题详情和答案>>
| 3 |
（1）操作：固定△ABC，将△C′D′E′绕点C顺时针旋转30°得到△CDE，连接AD、BE，CE的延长线交AB于F（图2）；
探究：在图2中，线段BE与AD之间有怎样的大小关系？试证明你的结论．
（2）操作：将图2中的△CDE，在线段CF上沿着CF方向以每秒1个单位的速度平移，平移后的△CDE设为△PQR（图3）；
请问：经过多少时间，△PQR与△ABC重叠部分的面积恰好等于
7
| ||
| 4 |
（3）操作：图1中△C′D′E′固定，将△ABC移动，使顶点C落在C′E′的中点，边BC交D′E′于点M，边AC交D′C′于点N，设
∠AC C′=α（30°＜α＜90，图4）；
探究：在图4中，线段C′N•E′M的值是否随α的变化而变化？如果没有变化，请你求出C′N•E′M的值，如果有变化，请你说明理由．
查看习题详情和答案>>
如图1是边长分别为4
和3的两个等边三角形纸片ABC和CDE叠放在一起．
（1）固定△ABC，将△CDE绕点C顺时针旋转30°得到△CDE，连接AD、BE、CE的延长线交AB于点F（图2），线段BE与AD之间有怎样的大小关系？证明你的结论；
（2）固定△CDE，将△ABC移动，使顶点C落在CE的中点G，边BG交DE于点M，边AG交DC于点N，求证：CN•EM=EG•CG；
（3）将图2中的△CDE，在线段CF上沿着CF方向以每秒1个单位的速度平移，平移后的△CDE设为△PQR（图4）；探究：设△PQR移动时间为x秒，△PQR与△ABC重叠部分的面积为y，求y与x之间的函数解析式，并写出函数自变量x的取值范围．
查看习题详情和答案>>
| 3 |
（1）固定△ABC，将△CDE绕点C顺时针旋转30°得到△CDE，连接AD、BE、CE的延长线交AB于点F（图2），线段BE与AD之间有怎样的大小关系？证明你的结论；
（2）固定△CDE，将△ABC移动，使顶点C落在CE的中点G，边BG交DE于点M，边AG交DC于点N，求证：CN•EM=EG•CG；
（3）将图2中的△CDE，在线段CF上沿着CF方向以每秒1个单位的速度平移，平移后的△CDE设为△PQR（图4）；探究：设△PQR移动时间为x秒，△PQR与△ABC重叠部分的面积为y，求y与x之间的函数解析式，并写出函数自变量x的取值范围．
图1是边长分别为4
和3的两个等边三角形纸片ABC和C′D′E′叠放在一起（C与C′重合）．
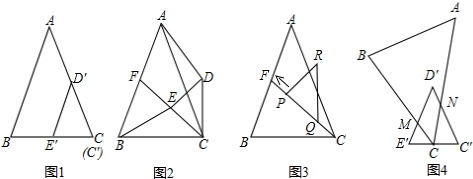
（1）操作：固定△ABC，将△C′D′E′绕点C顺时针旋转30°得到△CDE，连接AD、BE，CE的延长线交AB于F（图2）；
探究：在图2中，线段BE与AD之间有怎样的大小关系？试证明你的结论．
（2）操作：将图2中的△CDE，在线段CF上沿着CF方向以每秒1个单位的速度平移，平移后的△CDE设为△PQR（图3）；
探究：设△PQR移动的时间为x秒，△PQR与△ABC重叠部分的面积为y，求y与x之间的函数解析式，并写出函数自变量x的取值范围．
（3）操作：图1中△C′D′E′固定，将△ABC移动，使顶点C落在C′E′的中点，边BC交D′E′于点M，边AC交D′C′于点N，设∠AC C′=α（30°＜α＜90°（图4）；
探究：在图4中，线段C′N•E′M的值是否随α的变化而变化？如果没有变化，请你求出C′N•E′M的值，如果有变化，请你说明理由．
查看习题详情和答案>>
| 3 |
（1）操作：固定△ABC，将△C′D′E′绕点C顺时针旋转30°得到△CDE，连接AD、BE，CE的延长线交AB于F（图2）；
探究：在图2中，线段BE与AD之间有怎样的大小关系？试证明你的结论．
（2）操作：将图2中的△CDE，在线段CF上沿着CF方向以每秒1个单位的速度平移，平移后的△CDE设为△PQR（图3）；
探究：设△PQR移动的时间为x秒，△PQR与△ABC重叠部分的面积为y，求y与x之间的函数解析式，并写出函数自变量x的取值范围．
（3）操作：图1中△C′D′E′固定，将△ABC移动，使顶点C落在C′E′的中点，边BC交D′E′于点M，边AC交D′C′于点N，设∠AC C′=α（30°＜α＜90°（图4）；
探究：在图4中，线段C′N•E′M的值是否随α的变化而变化？如果没有变化，请你求出C′N•E′M的值，如果有变化，请你说明理由．
查看习题详情和答案>>
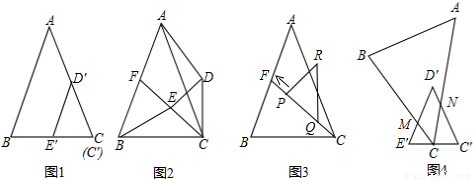
图1是边长分别为4
和3的两个等边三角形纸片ABC和C′D′E′叠放在一起（C与C′重合）．
（1）操作：固定△ABC，将△C′D′E′绕点C顺时针旋转30°得到△CDE，连接AD、BE，CE的延长线交AB于F（图2）；
探究：在图2中，线段BE与AD之间有怎样的大小关系？试证明你的结论．
（2）操作：将图2中的△CDE，在线段CF上沿着CF方向以每秒1个单位的速度平移，平移后的△CDE设为△PQR（图3）；
探究：设△PQR移动的时间为x秒，△PQR与△ABC重叠部分的面积为y，求y与x之间的函数解析式，并写出函数自变量x的取值范围．
（3）操作：图1中△C′D′E′固定，将△ABC移动，使顶点C落在C′E′的中点，边BC交D′E′于点M，边AC交D′C′于点N，设∠AC C′=α（30°＜α＜90°（图4）；
探究：在图4中，线段C′N•E′M的值是否随α的变化而变化？如果没有变化，请你求出C′N•E′M的值，如果有变化，请你说明理由．
查看习题详情和答案>>
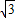和3的两个等边三角形纸片ABC和C′D′E′叠放在一起（C与C′重合）．（1）操作：固定△ABC，将△C′D′E′绕点C顺时针旋转30°得到△CDE，连接AD、BE，CE的延长线交AB于F（图2）；
探究：在图2中，线段BE与AD之间有怎样的大小关系？试证明你的结论．
（2）操作：将图2中的△CDE，在线段CF上沿着CF方向以每秒1个单位的速度平移，平移后的△CDE设为△PQR（图3）；
探究：设△PQR移动的时间为x秒，△PQR与△ABC重叠部分的面积为y，求y与x之间的函数解析式，并写出函数自变量x的取值范围．
（3）操作：图1中△C′D′E′固定，将△ABC移动，使顶点C落在C′E′的中点，边BC交D′E′于点M，边AC交D′C′于点N，设∠AC C′=α（30°＜α＜90°（图4）；
探究：在图4中，线段C′N•E′M的值是否随α的变化而变化？如果没有变化，请你求出C′N•E′M的值，如果有变化，请你说明理由．
查看习题详情和答案>>