网址：http://m.1010jiajiao.com/timu3_id_456483[举报]
在数学学习过程中，通常是利用已有的知识与经验，通过对研究对象进行观察、实验、推理、抽象概括，发现数学规律，揭示研究对象的本质特征。
比如“同底数幂的乘法法则”的学习过程是利用有理数的乘方概念和乘法结合律，由“特殊”到“一般”进行抽象概括的： 22×23＝25，23×24＝27，22×26＝28，…
2m×2n＝2m+n，…am×an＝am+n(m、n都是正整数)。探索问题：
（1）比较下列各组数据的大小：
①
， ② 
， ③ 
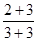， ④ 
，…。
(2)请你根据上面的材料归纳出a、b、c(a＞b＞0，c＞0)之间的一个数学关系式；并用已学的数学知识说明你发现结论的正确性.
(3)试用(2)中你归纳的数学关系式，解释下面生活中的一个现象：“若m克糖水里含有n克糖，再加入k克糖(仍不饱和)，则糖水更甜了”；
在数学学习过程中，通常是利用已有的知识与经验，通过对研究对象进行观察、实验、推理、抽象概括，发现数学规律，揭示研究对象的本质特征。
比如“同底数幂的乘法法则”的学习过程是利用有理数的乘方概念和乘法结合律，由“特殊”到“一般”进行抽象概括的： 22×23＝25，23×24＝27，22×26＝28，…
2m×2n＝2m+n，…am×an＝am+n(m、n都是正整数)。探索问题：
（1）比较下列各组数据的大小：
①
， ② 
， ③ 
， ④ 
，…。
(2)请你根据上面的材料归纳出a、b、c(a＞b＞0，c＞0)之间的一个数学关系式；并用已学的数学知识说明你发现结论的正确性.
(3)试用(2)中你归纳的数学关系式，解释下面生活中的一个现象：“若m克糖水里含有n克糖，再加入k克糖(仍不饱和)，则糖水更甜了”；
查看习题详情和答案>>
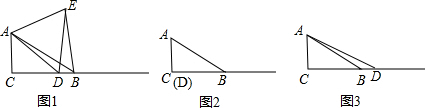
问题：如图1，在Rt△ABC中，∠C=90°，∠ABC=30°，点D是射线CB上任意一点，△ADE是等边三角形，且点D在∠ACB的内部，连接BE．探究线段BE与DE之间的数量关系．请你完成下列探究过程：先将图形特殊化，得出猜想，再对一般情况进行分析并加以证明．
（1）当点D与点C重合时（如图2），请你补全图形．由∠BAC的度数为______，点E落在______，容易得出BE与DE之间的数量关系为______；
（2）当点D在如图3的位置时，请你画出图形，研究线段BE与DE之间的数量关系是否与（1）中的结论相同，写出你的猜想并加以证明．
查看习题详情和答案>>
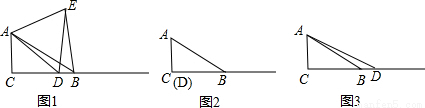
（1）当点D与点C重合时（如图2），请你补全图形．由∠BAC的度数为______，点E落在______，容易得出BE与DE之间的数量关系为______；
（2）当点D在如图3的位置时，请你画出图形，研究线段BE与DE之间的数量关系是否与（1）中的结论相同，写出你的猜想并加以证明．
查看习题详情和答案>>
问题背景：
如图1，在Rt△ABC中，∠C＝90°，∠ABC＝30°，点D是射线CB上任意一点，△ADE是等边三角形，且点E在∠ACB的内部，连接BE．试探究线段BE与DE之间的数量关系．
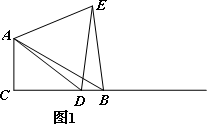
探究结论：
先将图形特殊化，得出猜想，再对一般情况进行分析并加以证明．
(1)当点D与点C重合时(如图2)，请你补全图形．由∠BAC的度数为________，点E落在AB上，容易得出BE与DE之间的数量关系为________；
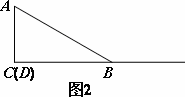
(2)当点D在如图3的位置时，请你画出图形，研究线段BE与DE之间的数量关系是否与(1)中的结论相同，写出你的猜想并加以证明．
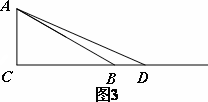
拓展应用：
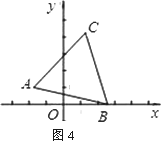
(3)如图4，在平面直角坐标系xOy中，点A的坐标为(
，1)，点B是x轴上的一动点，以AB为边作等边三角形ABC．当C(x，y)在第一象限内时，求y与x的函数关系式．
