题目内容
问题背景:
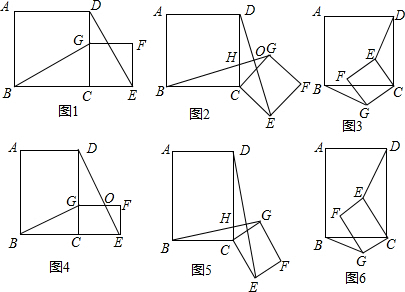
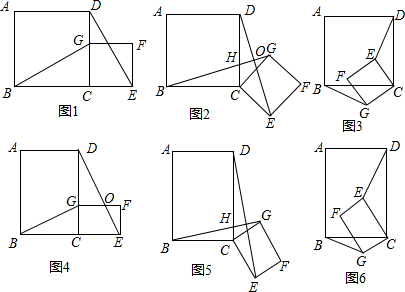
如图1,在Rt△ABC中,∠C=90°,∠ABC=30°,点D是射线CB上任意一点,△ADE是等边三角形,且点E在∠ACB的内部,连接BE.试探究线段BE与DE之间的数量关系.
探究结论:
先将图形特殊化,得出猜想,再对一般情况进行分析并加以证明.
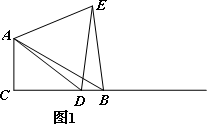
(1)当点D与点C重合时(如图2),请你补全图形.由∠BAC的度数为________,点E落在AB上,容易得出BE与DE之间的数量关系为________;
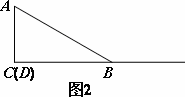
(2)当点D在如图3的位置时,请你画出图形,研究线段BE与DE之间的数量关系是否与(1)中的结论相同,写出你的猜想并加以证明.
拓展应用:
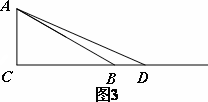
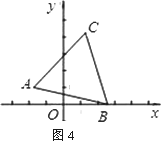
(3)如图4,在平面直角坐标系xOy中,点A的坐标为(![]() ,1),点B是x轴上的一动点,以AB为边作等边三角形ABC.当C(x,y)在第一象限内时,求y与x的函数关系式.
,1),点B是x轴上的一动点,以AB为边作等边三角形ABC.当C(x,y)在第一象限内时,求y与x的函数关系式.
解析:
|
(1)60°,BE=DE.(4分) (2)完成画图如图.猜想:
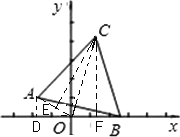
证明:取AB的中点F,连结EF. ∵ ∴ ∴△ ∴ ∵△ADE是等边三角形, ∴ ∴ ∴ 即 由①②③得△ACD≌△AFE(SAS). ∴ ∵F是AB的中点, ∴EF是AB的垂直平分线. ∴BE=AE. ∵△ADE是等边三角形, ∴DE=AE. ∴BE=DE.(4分) (3)如图,过A作AD⊥x轴,交x轴于D,由A(-
|

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案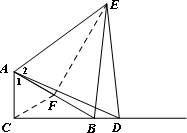
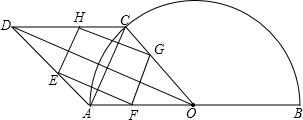 值,判断此时四边形EFGH的形状,并说明理由.
值,判断此时四边形EFGH的形状,并说明理由. (2011•临川区模拟)问题背景:如图1,四边形ABCD和CEFG都是正方形,B,C,E在同一条直线上,连接BG,DE.
(2011•临川区模拟)问题背景:如图1,四边形ABCD和CEFG都是正方形,B,C,E在同一条直线上,连接BG,DE.
 问题背景:如图1,四边形ABCD和CEFG都是正方形,B,C,E在同一条直线上,连接BG,DE.
问题背景:如图1,四边形ABCD和CEFG都是正方形,B,C,E在同一条直线上,连接BG,DE.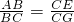 =k(其中k>0),请直接写出线段BG、DE的数量关系及位置关系.请选择图5或图6证明你的判断.
=k(其中k>0),请直接写出线段BG、DE的数量关系及位置关系.请选择图5或图6证明你的判断.