摘要：24．(1)作公切线 如图.C为线段AB上一点.以BC为直径作⊙O,再以AO为直径作⊙M交⊙O于D.E.过点B作AB的垂线交AD的延长线于F.连结CD. (1)若AC＝2.且AC与AD的长是关于的方程的两个根.①求证:AD是⊙O的切线,②求线段DF的长,③求sin∠ADC的值.(2)当点C是线段AB上的一动点.为何值时.△ACD是等腰三角形.
网址：http://m.1010jiajiao.com/timu3_id_455965[举报]
如图，B是线段AC上的一点，分别以AB、BC、AC为直径作半圆．过B作BD⊥AC，与较大半圆相交于D，以BD为直径的圆交两个较小半圆于E、F．求证：(1)四边形BEDF是矩形；(2)直线EF是以AB、BC为直径的两个半圆的公切线．
查看习题详情和答案>>
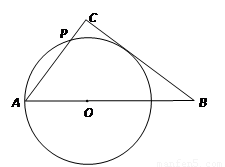
如图1，Rt△ABC中，∠ACB=90°，AC=3，BC=4，点O是斜边AB上一动点，以OA为半径作⊙O与AC边交于点P。
（1）当OA=
时，求点O到BC的距离；
（2）如图2，当OA=
时，求证：直线BC 与⊙O相切；此时线段AP的长是多少？
（3）若BC边与⊙O有公共点，直接写出 OA 的取值范围；
（4）若CO平分∠ACB，则线段AP的长是多少？
（1）当OA=
时，求点O到BC的距离；（2）如图2，当OA=
时，求证：直线BC 与⊙O相切；此时线段AP的长是多少？（3）若BC边与⊙O有公共点，直接写出 OA 的取值范围；
（4）若CO平分∠ACB，则线段AP的长是多少？
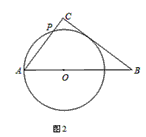
如图1，Rt△ABC中，∠ACB=90°，AC=3，BC=4，点O是斜边AB上一动点，以OA为半径作⊙O与AC边交于点P，
1.当OA=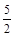
时，求点O到BC的距离
2.如图2，当OA=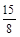
时，求证：直线BC与⊙O相切；此时线段AP的长是多少？
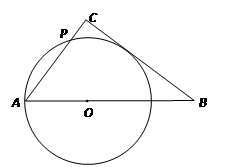
3.若BC边与⊙O有公共点，直接写出 OA
的取值范围；
4.若CO平分∠ACB，则线段AP的长是多少？
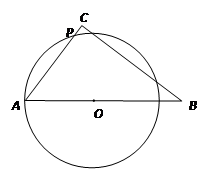
查看习题详情和答案>>
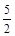时，求点O到BC的距离
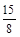时，求证：直线BC与⊙O相切；此时线段AP的长是多少？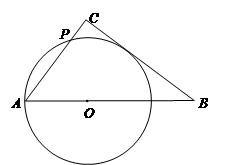
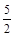时，求点O到BC的距离
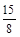时，求证：直线BC与⊙O相切；此时线段AP的长是多少？
