摘要:26.已知:如图.在四边形ABCD中.E为AB上一点.△ADE和△BCE都是等边三 角形.AB.BC.CD.DA的中点分别为P.Q.M.N.试判断四边形PQMN为怎样的四边形.并证明你的结论. [提示]连结AC和CD.首先利用中位线定理和平行四边形判定定理.证明四边形PQMN为平行四边形.然后证明△AEC≌△DEB.得到AC=BD.再证明□PQMN为菱形. [答案]四边形PQMN为菱形.证明如下: 如图.连结AC.BD. ∵ PQ为△ABC的中位线. ∴ PQ AC. 同理 MNAC. ∴ MNPQ. ∴ 四边形PQMN为平行四边形. 在△AEC和△DEB中. AE=DE.EC=EB.∠AED=60°=∠CEB. 即 ∠AEC=∠DEB. ∴ △AEC≌△DEB. ∴ AC=BD. ∴ PQ=AC=BD=PN. ∴ □PQMN为菱形.
网址:http://m.1010jiajiao.com/timu3_id_455364[举报]
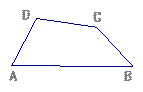
已知:如图,在四边形ABCD中,AD=BC,∠A、∠B均为锐角.
当∠A=∠B时,则CD与A B的位置关系是CD AB,大小关系是CD AB;
当∠A>∠B时,(1)中C D与A B的大小关系是否还成立,证明你的结论.
查看习题详情和答案>>
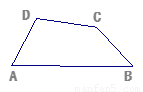
已知:如图,在四边形ABCD中,AD=BC,∠A、∠B均为锐角.
当∠A=∠B时,则CD与A B的位置关系是CD AB,大小关系是CD AB;
当∠A>∠B时,(1)中C D与A B的大小关系是否还成立,证明你的结论.
查看习题详情和答案>>
已知:如图,在四边形ABCD中, AD=BC,∠A、∠B均为锐角.
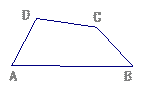
当∠A=∠B时,则CD与A B的位置关系是CD AB,大小关系是CD AB;
当∠A>∠B时,(1)中C D与A B的大小关系是否还成立,证明你的结论. 查看习题详情和答案>>

当∠A=∠B时,则CD与A B的位置关系是CD AB,大小关系是CD AB;
当∠A>∠B时,(1)中C D与A B的大小关系是否还成立,证明你的结论. 查看习题详情和答案>>