摘要:24.如图.在梯形ABCD中.AD∥BC.AB=DC.BD⊥DC于D.且∠C=60°.若 AD=5 cm.求梯形的腰长. [提示]求出∠CBD.∠ABD和∠ADC的度数.证明AB=AD.或者过D点作DE⊥BC于E.CE为下底与上底的差的一半.又是CD的一半.CD又是BC的一半.从中找出CD与AD的关系. [解法一]∵ BD⊥CD.∠C=60°. ∴ ∠CBD=30°. 在等腰梯形ABCD中.∠ABC=∠C=60°. ∴ ∠ABD=∠CBD=30°. ∵ AD∥BC. ∴ ∠ADB=∠CBD. ∴ ∠ABD=∠ADB. ∴ AB=AD=5(cm). [解法二]过D点作DE⊥BC.垂足为E点. ∵ 在Rt△CDE中.∠CDE=30°. ∴ CE=CD. 又 CE=(BC-AD). ∴ CD=BC-AD. 即 BC=CD+AD. 又 在Rt△BCD中.∠CBD=30°. ∴ CD=BC. ∴ CD=2 CD-AD. 即 CD=AD=5(cm).
网址:http://m.1010jiajiao.com/timu3_id_455362[举报]
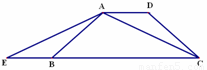
如图,在梯形ABCD中,AD∥BC,AB=DC,延长CB到E,使BE=AD,连接AE、AC.
(1)求证:AE=AC;
(2)若梯形ABCD的高为2,∠CAD=30°,求梯形ABCD的面积.
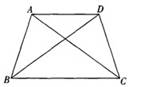
如图,在梯形ABCD中,AD//BC,AB=DC,过点D作DE⊥BC,垂足为E,并延长DE至F,使EF=DE.连接BF、AC.

(1)求证:四边形ABFC是平行四边形;
(2)如果DE2=BE·CE,求证四边形ABFC是矩形.
查看习题详情和答案>>