摘要：(1)证明:∵在△ABC与△EFD中,AB=EF,由EF∥AB得∠BAC=∠FED.由AD= CE得AC=ED. ∴△ABC≌△EFD. (2)四边形BDFC是平行四边形. 证明:∵△ABC≌△EFD, ∴BC=FD,∠BCA=∠EDF. ∴BC∥FD ∴四边形BDFC是平行四边形. 26剖析:解题时.注意区分判定定理与性质定理的不同使用. ∵□ 中.∥.∴. 又.. ∴△≌△.∴. ∴四边形是平行四边形 . 又.∴□ 是菱形.
网址：http://m.1010jiajiao.com/timu3_id_455235[举报]
如图，A，E，B，D，在同一直线上，在△ABC与△DEF中，AC=DF，AC∥DF．请添加一个条件，然后再正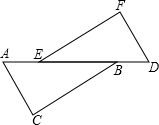
确得出BC=EF．
（1）你添加的条件是
（2）证明：BC=EF．
查看习题详情和答案>>
确得出BC=EF．（1）你添加的条件是
AB=DE
AB=DE
；（2）证明：BC=EF．
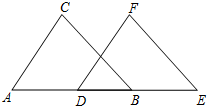
将下列说理过程补充完整 如图，点B、E、C、F在同一直线上，AB=DE，AC=DF，BE=CF．求证：∠A=∠D．
证明：∵BE=CF，
∴BE+CE=CF+CE，即
BC
BC
=EF
EF
（等式的性质）在△ABC与△DEF中
AB
AB
=DE
DE
AC
AC
=DF
DF
BC
BC
=EF
EF
∴△ABC≌△DEF（
SSS
SSS
）∴∠A=∠D（
全等三角形的对应角相等
全等三角形的对应角相等
）如图1，在△ABC与△BDE中，∠ABC=∠BDE=90°，BC=DE，AB=BD，M、M′分别为AB、BD中点．
（1）探索CM与EM′有怎样的数量关系？请证明你的结论；
（2）如图2，连接MM′并延长交CE于点K，试判断CK与EK之间的数量关系，并说明理由．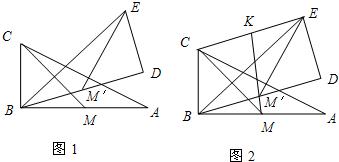
查看习题详情和答案>>
（1）探索CM与EM′有怎样的数量关系？请证明你的结论；
（2）如图2，连接MM′并延长交CE于点K，试判断CK与EK之间的数量关系，并说明理由．
19、如图，点A，E，B，D在同一直线上，在△ABC与△DEF中，AC=DF，AC∥DF，加一个条件使得△ABC≌△DEF，并证明增加条件为：
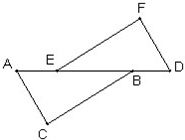
填空：把下面的推理过程补充完整，并在括号内注明理由．如图，点B、D在线段AE上，BC∥EF，AD=BE，BC=EF．
求证：（1）∠C=∠F；（2）AC∥DF．
证明：（1）∵BC∥EF（已知）
∴∠ABC=
∠E
∠E
（两直线平行同位角相等
两直线平行同位角相等
）∵AD=BE
∴AD+DB=DB+BE
即
AB
AB
=DE在△ABC与△DEF中
AB=DE
∠ABC=∠E
BC=EF（
已知
已知
）∴△ABC≌△DEF（
SAS
SAS
）∴∠C=∠F（
全等三角形的对应角相等
全等三角形的对应角相等
）（2）∵△ABC≌△DEF
∴∠A=∠FDE（
全等三角形的对应角相等
全等三角形的对应角相等
）∴AC∥DF（
同位角相等两直线平行
同位角相等两直线平行
）