摘要:22.如图(1).AB.CD是两条线段.M是AB的中点.S△DMC.S△DAC和S△DBC分别 表示△DMC.△DAC.△DBC的面积.当AB∥CD时.有 S△DMC= ① 中AB∥CD时.①式是否成立?请说明理由. 中AB与CD相交于点O时.S△DMC与S△DAC和S△DBC有何种相等关系?证明你的结论. 图 图(3) [提示]△DAC.△DMC 和△DBC 同底CD.通过它们在CD 边上的高的关系.来确定它们面积的关系. [答案](1)当AB∥CD时.①式仍成立. 分别过A.M.B作CD的垂线.AE.MN.BF的垂足分别为E.N.F. ∵ M为AB的中点. ∴ MN=(AE+BF). ∴ S△DAC+S△DBC=DC·AE+DC·BF=DC·(AE+BF)=2 S△DMC. ∴ S△DMC= 有S△DMC=. 证法一:∵ M是AB的中点.S△ADM=S△BDM.S△ACM=S△BCM. S△DBC=S△BDM+S△BCM+S△DMC. ① S△DAC=S△ADM+S△ACM-S△DMC ② ①-②得:S△DBC-S△DAC=2 S△DMC ∴ S△DMC=. 证法二:如右图.过A作CD的平行线l.MN⊥l.垂足为N.BE⊥l.垂足为E.设A.M.B到CD的距离分别h1.h0.h2.则MN=h1+h0.BE=h2+h1. ∵ AM=BM. ∴ BE=2 MN. ∴ h2+h1=2(h1+h0). ∴ h0=. ∴ S△DMC=.
网址:http://m.1010jiajiao.com/timu3_id_455184[举报]
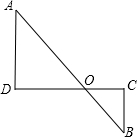 如图,四条线段的长分别为9,5,x、1(其中x为正实数),用它们拼成两个相似的直角三角形,且AB与CD是其中的两条线段,则x可取值的个数为( )
如图,四条线段的长分别为9,5,x、1(其中x为正实数),用它们拼成两个相似的直角三角形,且AB与CD是其中的两条线段,则x可取值的个数为( )| A、1个 | B、3个 | C、6个 | D、9个 |
如图,P是定长线段AB上一点,C、D两点分别从P、B出发以1cm/s、2cm/s的速度沿直线AB向左运动(C在线段AP上,D在线段BP上)
(1)若C、D运动到任一时刻时,总有PD=2AC,请说明P点在线段AB上的位置:

(2)在(1)的条件下,Q是直线AB上一点,且AQ-BQ=PQ,求
的值.

(3)在(1)的条件下,若C、D运动5秒后,恰好有CD=
AB,此时C点停止运动,D点继续运动(D点在线段PB上),M、N分别是CD、PD的中点,下列结论:①PM-PN的值不变;②
的值不变,可以说明,只有一个结论是正确的,请你找出正确的结论并求值.
 查看习题详情和答案>>
查看习题详情和答案>>
(1)若C、D运动到任一时刻时,总有PD=2AC,请说明P点在线段AB上的位置:

(2)在(1)的条件下,Q是直线AB上一点,且AQ-BQ=PQ,求
| PQ |
| AB |

(3)在(1)的条件下,若C、D运动5秒后,恰好有CD=
| 1 |
| 2 |
| MN |
| AB |
 查看习题详情和答案>>
查看习题详情和答案>>
如图,直线y=-2x+2与x轴、y轴分别交于A、B两点,将△OAB绕点O逆时针方向旋转90°后得到△OCD.
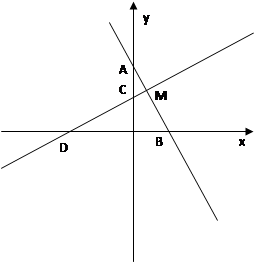
(1)填空:点C的坐标是( , ),点D的坐标是( , );
(2)设直线CD与AB交于点M,求线段BM的长;
(3)在y轴上是否存在点P,使得△BMP是等腰三角形?若存在,请求出所有满足条件的点P的坐标;若不存在,请说明理由.
查看习题详情和答案>>

