摘要：18．如图.E是矩形ABCD的边AD上一点.且BE＝ED.P是对角线BD上任意一点.PF⊥BE.PG⊥AD.垂足分别为F.G．求证:PF+PG＝AB． [提示]延长GP交BC于H.只要证PH＝PF即可.所以只要证∠PBF＝∠PBH． [答案]∵ BE＝DE. ∴ ∠EBD＝∠EDB． ∵ 在矩形ABCD中.AD∥BC. ∴ ∠DBC＝∠ADB. ∴ ∠EBD＝∠CBD． 延长GP交BC于H点． ∵ PG⊥AD. ∴ PH⊥BC． ∵ PF⊥BE.P是∠EBC的平分线上． ∴ PF＝PH． ∵ 四边形ABHG中. ∠A＝∠ABH＝∠BHG＝∠HGA＝90°． ∴ 四边形ABHG为矩形. ∴ AB＝GH＝GP+PH＝GP+PF 故 PF+PG＝AB．
网址：http://m.1010jiajiao.com/timu3_id_455180[举报]
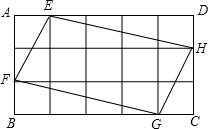
如图，将矩形ABCD分成15个大小相等的正方形，E、F、G、H分别在AD、AB、BC、CD边上，且是某个小正方形的顶点．若一只小猫在这个图形上玩耍，则落在四边形EFGH内的概率是 ．
查看习题详情和答案>>
查看习题详情和答案>>
如图，在矩形ABCD中，AB=8cm，AD=6cm，点F是CD延长线上一点，且DF=2cm．点P、Q分别从A、C同时出发，以1cm/s的速度分别沿边AB、CB向终点B运动，当一点运动到终点B时，另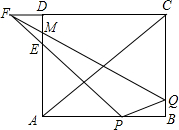
一点也停止运动．FP、FQ分别交AD于E、M两点，连接PQ、AC，设运动时间为t （s）．
（1）用含有t的代数式表示DM的长；
（2）设△FCQ的面积为y （cm2），求y与t之间的函数关系式；
（3）线段FQ能否经过线段AC的中点？若能，请求出此时t的值；若不能，请说明理由；
（4）设△FPQ的面积为S （cm2），求S与t之间的函数关系式，并回答：在t的取值范围内，S是如何随t的变化而变化的？ 查看习题详情和答案>>
一点也停止运动．FP、FQ分别交AD于E、M两点，连接PQ、AC，设运动时间为t （s）．（1）用含有t的代数式表示DM的长；
（2）设△FCQ的面积为y （cm2），求y与t之间的函数关系式；
（3）线段FQ能否经过线段AC的中点？若能，请求出此时t的值；若不能，请说明理由；
（4）设△FPQ的面积为S （cm2），求S与t之间的函数关系式，并回答：在t的取值范围内，S是如何随t的变化而变化的？ 查看习题详情和答案>>
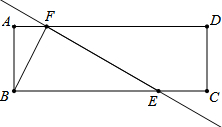如图，在矩形ABCD中，AB=1，BC=3，F为线段AD上一点（不与端点A，D重合），过F的直线交矩形的另一边于点E，且该直线满足tan∠DFE=| 1 | 2 |
（1）记△BEF的面积为S，求S与x的函数关系式；
（2）当点E在线段BC上时，若矩形ABCD关于直线EF的对称图形为矩形A′B′C′D′，试说明矩形ABCD与矩形A′B′C′D′的重叠部分的面积是否发生变化？若不变，求出重叠部分的面积；若改变，请说明理由．
如图，在矩形ABCD中，点E是CD的中点，点F是边AD上一点，连结FE并廷长交BC的延长线于点G，连接BF、BE。且BE⊥FG;
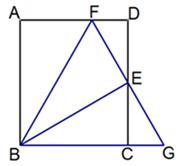
（1）求证：BF=BG。
（2）若tan∠BFG=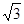
，S△CGE=6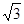，求AD的长。
（1）求证：BF=BG。
（2）若tan∠BFG=
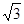，S△CGE=6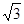，求AD的长。
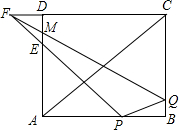一点也停止运动．FP、FQ分别交AD于E、M两点，连接PQ、AC，设运动时间为t （s）．