摘要:如图.四边形ABCD为矩形.AB=4.AD=3.动点M.N分别从D.B同时出发.以1个单位/秒的速度运动.点M沿DA向终点A运动.点N沿BC向终点C运动.过点N作NP⊥BC.交AC于点P.连结MP.已知动点运动了秒. ⑴请直接写出PN的长,(用含的代数式表示) ⑵若0秒≤≤1秒.试求△MPA的面积S与时间秒的函数关系式.利用函数图象.求S的最大值. ⑶若0秒≤≤3秒.△MPA能否为一个等腰三角形?若能.试求出所有的对应值,若不能.试说明理由. 解:⑴, ⑵延长NP交AD于点Q.则PQ⊥AD.由⑴得:PN=. 则. 依题意.可得: ∵0≤≤1.5 即函数图象在对称轴的左侧.函数值S 随着的增大而增大. ∴当时.S有最大值 .S最大值=. ⑶△MPA能成为等腰三角形. 共有三种情况.以下分类说明: ①若PM=PA. ∵PQ⊥MA ∴MQ=QA= 又DM+MQ+QA=AD ∴.即 ②若MP=MA.则MQ=.PQ=.MP=MA= 在Rt△PMQ中.由勾股定理得: ∴.解得:(不合题意.舍去) ③若AP=AM. 由题意可得:.AM= ∴.解得: 综上所述.当.或.或时.△MPA是等腰三角形.
网址:http://m.1010jiajiao.com/timu3_id_455120[举报]
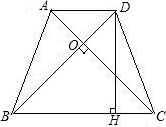 如图,四边形ABCD为等腰梯形,AD∥BC,AB=CD,对角线AC、BD交于点O,且AC⊥BD,DH⊥BC.
如图,四边形ABCD为等腰梯形,AD∥BC,AB=CD,对角线AC、BD交于点O,且AC⊥BD,DH⊥BC.(1)求证:DH=
| 1 | 2 |
(2)若AC=6,求梯形ABCD的面积. 查看习题详情和答案>>
 (2013•泰安)如图,四边形ABCD为正方形.点A的坐标为(0,2),点B的坐标为(0,-3),反比例函数y=
(2013•泰安)如图,四边形ABCD为正方形.点A的坐标为(0,2),点B的坐标为(0,-3),反比例函数y=| k | x |
(1)求反比例函数与一次函数的解析式;
(2)求点P是反比例函数图象上的一点,△OAP的面积恰好等于正方形ABCD的面积,求P点的坐标.
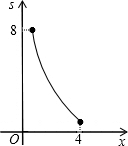
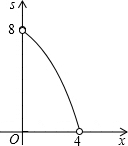
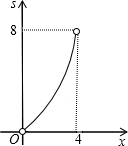
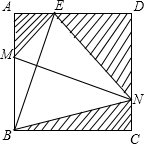 如图,四边形ABCD为正方形,若AB=4,E是AD边上一点(点E与点A、D不重合),BE的中垂线交AB于M,交DC于N,设AE=x,则图中阴影部分的面积S与x的大致图象是( )
如图,四边形ABCD为正方形,若AB=4,E是AD边上一点(点E与点A、D不重合),BE的中垂线交AB于M,交DC于N,设AE=x,则图中阴影部分的面积S与x的大致图象是( )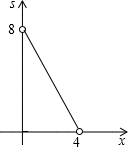
 如图,四边形ABCD为矩形纸片.把纸片ABCD折叠,使点B恰好落在CD边的中点E处,折痕为AF.若CD=6,则AF等于
如图,四边形ABCD为矩形纸片.把纸片ABCD折叠,使点B恰好落在CD边的中点E处,折痕为AF.若CD=6,则AF等于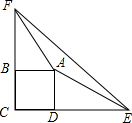 已知:如图,四边形ABCD为正方形,E、F分别为CD、CB延长线上的点,且DE=BF.
已知:如图,四边形ABCD为正方形,E、F分别为CD、CB延长线上的点,且DE=BF.