摘要：如图.在平面直角坐标系中.四边形ABCO是正方形.点C的坐标是(4.0). (1)直接写出A.B两点的坐标.A B (2)若E是BC上一点且∠AEB=60°.沿AE折叠正方形ABCO.折叠后点B落在平面内点F处.请画出点F并求出它的坐标. (3)若E是直线BC上任意一点.问是否存在这样的点E.使正方形ABCO沿AE折叠后.点B恰好落在轴上的某一点P处?若存在.请写出此时点P与点E的坐标,若不存在.请说明理由.
网址：http://m.1010jiajiao.com/timu3_id_454879[举报]
如图，在平面直角坐标系中，四边形OABC是矩形，OA=4，AB=2，直线y=-x+| 3 | 2 |
（1）求M、D两点的坐标；
（2）当P在什么位置时，PA=PB求出此时P点的坐标；
（3）过P作PH⊥BC，垂足为H，当以PM为直径的⊙F与BC相切于点N时，求梯形PMBH的面积． 查看习题详情和答案>>
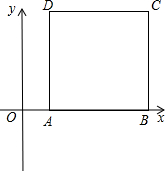如图，在平面直角坐标系中，四边形ABCD是边长为8的正方形，OA=2，求：（1）写出A、B、C、D各点的坐标；
（2）若正方形ABCD的两条对角线相交于点P，请求出经过O、P、B三点的抛物线的解析式；
（3）在（2）中的抛物线上，是否存在一点Q，使△QAB的面积为16？如果存在，请求出Q点的坐标；如果不存在，请说明理由． 查看习题详情和答案>>
如图，在平面直角坐标系中，四边形OABC是矩形，OA=3，AB=4，将线段OA绕点O顺时针旋转90°，使点A落在OC边上的点E处，抛物线y=ax2+bx+c过A，E，B三点．
（1）求抛物线的解析式；
（2）若M为抛物线的对称轴上一动点，当△MBE的周长最小时，求M点的坐标；
（3）点P从A点出发，以每秒1个单位长度的速度沿AB向B点运动，同时点Q从点B出发，以每秒1个单位长度的速度沿BO向点O运动．P点到达终点B时，Q点同时停止运动，运动时间为t（秒）．设△PBQ的面积为S，求S与t之间的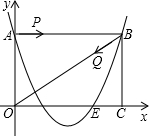
函数关系式．
查看习题详情和答案>>
（1）求抛物线的解析式；
（2）若M为抛物线的对称轴上一动点，当△MBE的周长最小时，求M点的坐标；
（3）点P从A点出发，以每秒1个单位长度的速度沿AB向B点运动，同时点Q从点B出发，以每秒1个单位长度的速度沿BO向点O运动．P点到达终点B时，Q点同时停止运动，运动时间为t（秒）．设△PBQ的面积为S，求S与t之间的
函数关系式．
查看习题详情和答案>>
15、如图，在平面直角坐标系中，四边形ABCD的四个顶点的坐标分别是A（1，3）、B（2，2）、C（2，1），D（3，3）．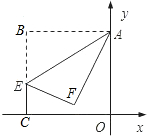
如图，在平面直角坐标系中，四边形OABC是正方形，A点坐标为（0，2），E是线段BC上一点，且∠AEB=60°，沿AE折叠后B点落在点F处，那么点F的坐标是