摘要:17.如图.在平面直角坐标系中.O为坐标原点.B(5.0).M为等腰梯形OBCD底边OB上一点.OD=BC=2.∠DMC=∠DOB=60°. (1)求直线CB的解析式: (2)求点M的坐标, (3)∠DMC绕点M顺时针旋转α后.得到∠D1MC1(点D1.C1依次与点D.C对应).射线MD1交直线DC于点E.射线MC1交直线CB于点F.设DE=m.BF=n. 求m与n的函数关系式. 解:(1)过点C作CA⊥OB.垂足为A.在Rt△ABC中.∠CAB=90°.∠CBO=60°. 0D=BC=2.∴CA=BC·sin∠CBO=, BA=BC·cos∠CBO=1. ∴点C的坐标为(4.). 设直线CB的解析式为y=kx+b.由B(5.0).C(4.). 得 解得 ∴直线CB的解析式为y=-x+5. (2)∵∠CBM+∠2+∠3=180°.∠DMC+∠1+∠2=180°.∠CBM=∠DMC=∠DOB=60° ∴∠2+∠3=∠1+∠2,∴∠1=∠3. ∴△ODM∽△BMC. ∴OD·BC=BM·OM. ∵B点为(5.0).∴OB=5. 设OM=x.则BM=5-x. ∵OD=BC=2.∴2×2=x(5-x). 解得x1=1.x2=4. ∴M点坐标为. 时. 如图①.OM=1.BM=4. ∵DC∥OB.∴∠MDE=∠DMO. 又∠DMO=∠MCB,∴∠MDE=∠MCB. ∵∠DME=∠CMF=a,∴△DME∽△CMF. ∴CF=2DE. ∵CF=2+n.DE=m. ∴2+n=2m.即m=1+. 时.如图②. OM=4,BM=1. 同理可得△DME∽△CMF. ∴DE=2CF. ∵CF=2-n.DE=m.∴m=2(2-n).即m=4-2n(<n<1).
网址:http://m.1010jiajiao.com/timu3_id_454607[举报]
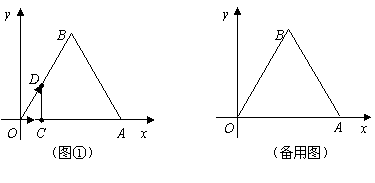
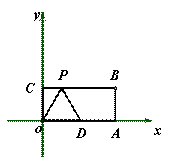
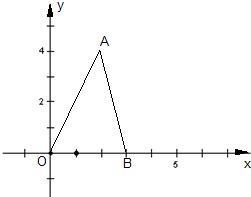 19、如图,在平面直角坐标系中,点A的坐标为(2,4),点B的坐标为(3,0).把△AOB沿射线OB的方向平移2个单位,其中A、O、B的对应点分别为D、E、F.
19、如图,在平面直角坐标系中,点A的坐标为(2,4),点B的坐标为(3,0).把△AOB沿射线OB的方向平移2个单位,其中A、O、B的对应点分别为D、E、F.