Question

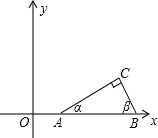如图，已知点A（tanα，0），B（tanβ，0）在x轴正半轴上，点A在点B的左边，α、β是以线段AB为斜边、顶点C在x轴上方的Rt△ABC的两个锐角．
（1）若二次函数y=-x²-

5

2

kx+（2+2k-k²）的图象经过A、B两点，求它的解析式；
（2）点C在（1）中求出的二次函数的图象上吗？请说明理由．

Answer 1

分析：（1）在Rt△ABC中，由于∠α+∠β=90°，因此tanα•anβ=1，而A、B是抛物线与x轴的交点，根据韦达定理可得出tanα•tanβ=-（2+2k-k²）=1，据此可求出k的值，然后根据tanα+tanβ＞0，将不合题意的k值舍去，即可求出抛物线的解析式．
（2）本题的关键是求出C点坐标，根据（1）可求出tanα、tanβ的值，以及A、B的坐标，过C作CD⊥AB，可在直角三角形ACD中，用tanα和CD表示出AD，同理可表示出BD的长，根据A、B的坐标可得出AB的长，根据AD+BD=AB即可求出CD的长，进而可求出AD和OD的长，即可得出C点坐标，代入抛物线的解析式中进行判断即可．

解答：解：（1）∵α、β是Rt△ABC的两个锐角，
∴tanα•tanβ=1，tanα＞0，tanβ＞0，
由题意，知tanα，tanβ是方程-x²-

5

2

kx+（2+2k-k²）=0的两个根．
∴tanα•tanβ=-（2+2k-k²）=k²-2k-2=1，
∴k²-2k-2=1，
解得，k=3或k=-1；
而tanα+tanβ=-

5

2

k＞0．
∴k＜0．
∴k=3（舍去），k=-1．
故所求的二次函数的解析式为y=-x²+

5

2

x-1．

（2）不存在．
过C作CD⊥AB于D．
令y=0，得-x²+

5

2

x-1=0．
解得x₁=

1

2

，x₂=2．
∴A（

1

2

，0），B（2，0），AB=

3

2

∴tanα=

1

2

，tanβ=2．
设CD=m，则有CD=AD•tanα=

1

2

AD，
∴AD=2CD．
又∵CD=BD•tanβ=2BD，
∴BD=

1

2

CD，
∴2m+

1

2

m=

3

2

，
∴m=

3

5

，
∴AD=

6

5

．
∴C（

17

10

，

3

5

），
当x=

17

10

时，y=

9

25

≠

3

5

．
∴点C不在（1）求出的二次函数的图象上．

点评：本题以二次函数为背景，考查了三角函数、韦达定理等相关知识点．综合性较强，难度适中．