网址:http://m.1010jiajiao.com/timu3_id_454178[举报]
(本题满分12分)
如图所示,在平面直角坐标系中,顶点为(![]() ,
,![]() )的抛物线交
)的抛物线交![]() 轴于
轴于![]() 点,交
点,交![]() 轴于
轴于![]() ,
,![]() 两点(点
两点(点![]() 在点
在点![]() 的左侧),已知
的左侧),已知![]() 点坐标为(
点坐标为(![]() ,
,![]() ).
).

(1)求此抛物线的解析式;
(2)过点![]() 作线段
作线段![]() 的垂线交抛物线于点
的垂线交抛物线于点![]() ,
,
如果以点![]() 为圆心的圆与直线
为圆心的圆与直线![]() 相切,请判断抛物
相切,请判断抛物
线的对称轴![]() 与⊙
与⊙![]() 有怎样的位置关系,并给出证明;
有怎样的位置关系,并给出证明;
(3)已知点![]() 是抛物线上的一个动点,且位于
是抛物线上的一个动点,且位于![]() ,
,
![]() 两点之间,问:当点
两点之间,问:当点![]() 运动到什么位置时,
运动到什么位置时,![]() 的
的
面积最大?并求出此时![]() 点的坐标和
点的坐标和![]() 的最大面积.
的最大面积.
查看习题详情和答案>>
(本题满分12分)如图甲,分别以两个彼此相邻的正方形?OABC与CDEF的边OC、OA所在直线为x轴、y轴建立平面直角坐标系(O、C、F三点在x轴正半轴上).若⊙P过A、B、E三点(圆心在x轴上),抛物线y=14x2+bx+c经过A、C两点,与x轴的另一交点为G,M是FG的中点,正方形CDEF的面积为1.
1.(1)求B点坐标;
2.(2)求证:ME是⊙P的切线;
3.(3)设直线AC与抛物线对称轴交于N,Q点是此对称轴上不与N点重合的一动点,①求△ACQ周长的最小值;
②若FQ=t,S△ACQ=S,直接写出S与t之间的函数关系式.
查看习题详情和答案>>
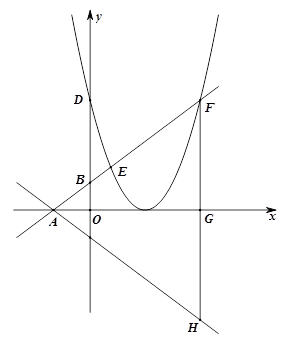
(本题满分12分)如图,在平面直角坐标系中,直线l:![]() 沿x轴翻折后,与x轴交于点A,与y轴交于点B,抛物线
沿x轴翻折后,与x轴交于点A,与y轴交于点B,抛物线![]() 与y轴交于点D,与直线AB交于点E、点F(点F在点E的右侧).
与y轴交于点D,与直线AB交于点E、点F(点F在点E的右侧).
(1)求直线AB的解析式;
(2)若线段DF∥x轴,求抛物线的解析式;
(3)如图,在(2)的条件下,过F作FH⊥x轴于点G,与直线l交于点H,在抛物线上是否存在P、Q两点(点P在点Q的上方),PQ与AF交于点M,与FH交于点N,使得直线PQ既平分△AFH的周长,又平分△AFH面积,如果存在,求出P、Q的坐标,若不存在,请说明理由.

查看习题详情和答案>>



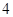 ,
,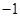 )的抛物线交
)的抛物线交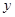 轴于
轴于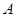 点,交
点,交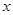 轴于
轴于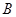 ,
,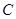 两点(点
两点(点 ,
,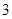 ).
).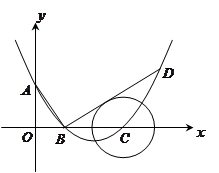
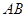 的垂线交抛物线于点
的垂线交抛物线于点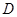 ,
,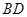 相切,请判断抛物
相切,请判断抛物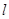 与⊙
与⊙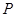 是抛物线上的一个动点,且位于
是抛物线上的一个动点,且位于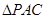 的
的