摘要：8．如图1.正方形ABCD和正方形BEFC. 操作:M是线段AB上一动点.从A点至B点移动.DM⊥MN.交对角线BF于点N. 探究:线段DM和MN之间的关系.并加以证明. 说明:如果你经历反复探索.没有找到解决问题的方法.请你把探索过程中的某种思路过程写出来在你经历说明(1)的过程之后.可以从下列①.②中选取一个补充或更换已知条件.完成你的证明.注意:选取①完成证明得9分,选取②完成证明得6分.①M是线段AB的中点,②M.N分别是线段AB.BF的中点. 附加题 如图2.当M是线段AE延长线上一动点.DM⊥MN.交对角线BF延长线于点N.探究线段DM和MN之间的关系.并加以证明. [课后作业] (19)矩形.菱形.正方形
网址：http://m.1010jiajiao.com/timu3_id_454033[举报]
（2007•中山区二模）（1）如图1，点B、M、C在同一直线上，以BM、BC为一边，在直线BC的两侧作等边△ABC和等边△BMN，直线AM、CN交于点O，则∠AOC=
（2）如图2，把△BMN绕点B逆时针旋转任意角度，∠AOC的度数是否变化，验证你的结论；
（3）如图3，正方形ABCD和正方形BMNE有公共顶点B，把正方形BMNE绕点B旋转任意角度，AM、CN交于点O，求∠AOC的度数．
查看习题详情和答案>>
60
60
度（直接写出答案）；（2）如图2，把△BMN绕点B逆时针旋转任意角度，∠AOC的度数是否变化，验证你的结论；
（3）如图3，正方形ABCD和正方形BMNE有公共顶点B，把正方形BMNE绕点B旋转任意角度，AM、CN交于点O，求∠AOC的度数．
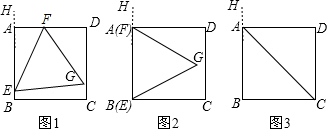
如图1，正方形ABCD和正三角形EFG的边长都为1，点E，F分别在线段AB，AD上滑动，设点G到CD的距离为x，到BC的距离为y，记∠HEF为α（当点E，F分别与B，A重合时，记α=0°）．
（1）当α=0°时（如图2所示），求x，y的值（结果保留根号）；
（2）当α为何值时，点G落在对角形AC上？请说出你的理由，并求出此时x，y的值（结果保留根号）；
（3）请你补充完成下表（精确到0.01）：
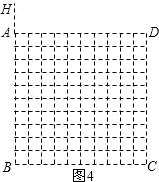
（4）若将“点E，F分别在线段AB，AD上滑动”改为“点E，F分别在正方形ABCD边上滑动”．当滑动一周时，请使用（3）的结果，在图4中描出部分点后，勾画出点G运动所形成的大致图形．
（参考数据：
≈1.732，sin15°=
≈0.259，sin75°=
≈0.966）
查看习题详情和答案>>
（1）当α=0°时（如图2所示），求x，y的值（结果保留根号）；
（2）当α为何值时，点G落在对角形AC上？请说出你的理由，并求出此时x，y的值（结果保留根号）；
（3）请你补充完成下表（精确到0.01）：
| α | 0° | 15° | 30° | 45° | 60° | 75° | 90° |
| x | 0.03 | 0 | 0.29 | ||||
| y | 0.29 | 0.13 | 0.03 |
（参考数据：
| 3 |
| ||||
| 4 |
| ||||
| 4 |
查看习题详情和答案>>
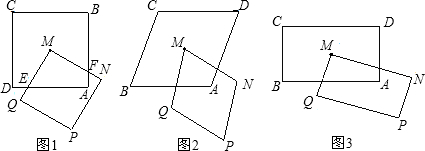
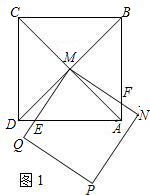
如图1，正方形ABCD和正方形QMNP，M是正方形ABCD的对称中心，MN交AB于F，QM交AD于E．
（1）猜想：ME与MF的数量关系；
（2）如图2，若将原题中的“正方形”改为“菱形”，且∠M=∠B，其它条件不变，探索线段ME与线段MF的数量关系，并加以证明；
（3）如图3，若将原题中的“正方形”改为“矩形”，且AB：BC=1：2，其它条件不变，探索线段ME与线段MF的数量关系，并说明理由；
（4）如图4，若将原题中的“正方形”改为平行四边形，且∠M=∠B，AB：BC=m，其它条件不变，求出ME：MF的值．（直接写出答案）
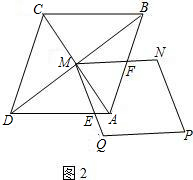
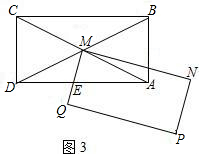
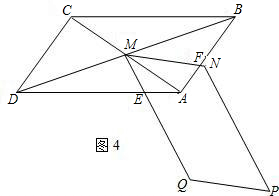查看习题详情和答案>>
（1）猜想：ME与MF的数量关系；
（2）如图2，若将原题中的“正方形”改为“菱形”，且∠M=∠B，其它条件不变，探索线段ME与线段MF的数量关系，并加以证明；
（3）如图3，若将原题中的“正方形”改为“矩形”，且AB：BC=1：2，其它条件不变，探索线段ME与线段MF的数量关系，并说明理由；
（4）如图4，若将原题中的“正方形”改为平行四边形，且∠M=∠B，AB：BC=m，其它条件不变，求出ME：MF的值．（直接写出答案）
查看习题详情和答案>>
