摘要:26.已知P 是抛物线y = ax2上的点.且点P在第一象限. (1)求m的值, (2)直线 y = kx +b过点P.交x轴的正半轴于点A.交抛物线于另一点M. ① 当b = 2a时.∠OPA=90°是否成立?如果成立.请证明,如果不成立.举出一个反例说明, ② 当b=4时.记△MOA的面积为S.求的最大值.
网址:http://m.1010jiajiao.com/timu3_id_453831[举报]
已知,抛物线y=ax2+4ax+t与x轴的一个交点为A(-1,0)
(1)求抛物线与x轴的另一个交点B的坐标;
(2)D是抛物线与y轴的交点,C是抛物线上的一点,且以AB为一底的梯形ABCD的面积为9,求此抛物线的解析式;
(3)E是第二象限内到x轴、y轴的距离的比为5∶2的点,如果点E在(2)中的抛物线上,且它与点A在此抛物线对称轴的同侧,问:在抛物线的对称轴上是否存在点P,使△APE的周长最小?若存在,求出点P的坐标,若不存在,请说明理由.
查看习题详情和答案>>已知:抛物线y=ax2+4ax+t与x轴的一个交点为A(-1,0).
⑴求抛物线与x轴的另一个交点B的坐标.
⑵点D是抛物线与y轴的交点,点C是抛物线上的一点,且以AB为一底的梯形ABCD的面积为9,求此抛物线的解析式.
⑶点E是第二象限内到x轴、y轴的距离的比为5∶2的点,如果点E在⑵中的抛物线上,且它与点A在此抛物线对称轴的同侧,问:在抛物线的对称轴上是否存在点P,使△APE的周长最小?若存在,求出点P的坐标;若不存在,请说明理由.
已知P(m,a)是抛物线y=ax2上的点,且点P在第一象限.
(1)求m的值
(2)直线y=kx+b过点P,交x轴的正半轴于点A,交抛物线于另一点M.
①当b=2a时,∠OPA=90°是否成立?如果成立,请证明;如果不成立,举出一个反例说明;
②当b=4时,记△MOA的面积为S,求
的最大值.
查看习题详情和答案>>
(1)求m的值
(2)直线y=kx+b过点P,交x轴的正半轴于点A,交抛物线于另一点M.
①当b=2a时,∠OPA=90°是否成立?如果成立,请证明;如果不成立,举出一个反例说明;
②当b=4时,记△MOA的面积为S,求
| 1 | s |
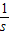 的最大值.
的最大值. 的最大值.
的最大值.