摘要:3.乘法公式及几何意义 [例4]化简 2 [例5]如图6.在边长为a的正方形中剪去一个边长为b的小正方形.把剩下的部分拼成一个梯形.分别计算这两个图形阴影部分的面积.验证了公式_____.
网址:http://m.1010jiajiao.com/timu3_id_453588[举报]
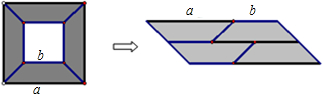
如图:边长为a,b的两个正方形,边保持平行,如果从大正方形中剪去小正方形,剩下的图形可以分割成4个大小相等的梯形.请你计算出两个阴影部分的面积,同时说明可以验证哪一个乘法公式的几何意义.

查看习题详情和答案>>

如图:边长为a,b的两个正方形,边保持平行,如果从大正方形中剪去小正方形,剩下的图形可以分割成4个大小相等的梯形.请你计算出两个阴影部分的面积,同时说明可以验证哪一个乘法公式的几何意义.
查看习题详情和答案>>
拼图游戏与代数恒等式
我们很喜欢拼图游戏,比如七巧板、俄罗斯方块等.它们不仅展现给我们丰富多彩的图案,还教给我们许多数学知识.教材中已用图1和图2解释了代数恒等式.
图1可以用来解释:(2a)2=4a2;
图2可以用来解释:(a+b)2=a2+2ab+b2.

很有趣吧!下面让我们一起来自制材料做一些拼图游戏.
准备工作:请尽可能多地做一些如下图所示的正方形和长方形的硬纸片.

探索研究:
(1)拼一些长方形或正方形,并用所拼成的图形面积来说明所学的乘法公式及某些幂的运算公式的正确性.
(2)拼出下列图形,利用面积的不同表示方法写出一个代数恒等式.

(3)哪些形式的代数恒等式可以用拼图求面积的方法来说明?
查看习题详情和答案>>23、乘法公式的探究及应用.
(1)如左图,可以求出阴影部分的面积是
(2)如右图,若将阴影部分裁剪下来,重新拼成一个长方形,它的宽是
(3)比较左、右两图的阴影部分面积,可以得到乘法公式
(4)运用你所得到的公式,计算下列各题:
①10.3×9.7
②(2m+n-p)(2m-n+p)

查看习题详情和答案>>
(1)如左图,可以求出阴影部分的面积是
a2-b2
(写成两数平方差的形式); (2)如右图,若将阴影部分裁剪下来,重新拼成一个长方形,它的宽是
a-b
,长是a+b
,面积是(a+b)(a-b)
.(写成多项式乘法的形式)(3)比较左、右两图的阴影部分面积,可以得到乘法公式
(a+b)(a-b)=a2-b2
.(用式子表达)(4)运用你所得到的公式,计算下列各题:
①10.3×9.7
②(2m+n-p)(2m-n+p)

28、问题1:同学们已经体会到灵活运用乘法公式给整式乘法及多项式的因式分解带来的方便,快捷.相信通过下面材料的学习探究,会使你大开眼界并获得成功的喜悦.
例:用简便方法计算195×205.
解:195×205
=(200-5)(200+5) ①
=2002-52 ②
=39975
(1)例题求解过程中,第②步变形是利用
(2)用简便方法计算:9×11×101×10001(4分)
问题2:对于形如x2+2xa+a2这样的二次三项式,可以用公式法将它分解成(x+a)2的形式.但对于二次三项式x2+2xa-3a2,就不能直接运用公式了.
此时,我们可以在二次三项式x2+2xa-3a2中先加上一项a2,使它与x2+2xa的和成为一个完全平方式,再减去a2,整个式子的值不变,于是有:x2+2xa-3a2=(x2+2ax+a2)-a2-3a2=(x+a)2-4a2=(x+a)2-(2a)2=(x+3a)(x-a)
像这样,先添一适当项,使式中出现完全平方式,再减去这个项,使整个式子的值不变的方法称为“配方法”.
利用“配方法”分解因式:a2-6a+8.
查看习题详情和答案>>
例:用简便方法计算195×205.
解:195×205
=(200-5)(200+5) ①
=2002-52 ②
=39975
(1)例题求解过程中,第②步变形是利用
平方差公式
(填乘法公式的名称).(2)用简便方法计算:9×11×101×10001(4分)
问题2:对于形如x2+2xa+a2这样的二次三项式,可以用公式法将它分解成(x+a)2的形式.但对于二次三项式x2+2xa-3a2,就不能直接运用公式了.
此时,我们可以在二次三项式x2+2xa-3a2中先加上一项a2,使它与x2+2xa的和成为一个完全平方式,再减去a2,整个式子的值不变,于是有:x2+2xa-3a2=(x2+2ax+a2)-a2-3a2=(x+a)2-4a2=(x+a)2-(2a)2=(x+3a)(x-a)
像这样,先添一适当项,使式中出现完全平方式,再减去这个项,使整个式子的值不变的方法称为“配方法”.
利用“配方法”分解因式:a2-6a+8.