摘要：4．解:(1)可设. ∵交y轴于点C(0.3).∴3＝16a-1.∴. ∴抛物线的解析式为.即. (2)存在 当y＝0时.则.∴∴A. 设P(0,m).则OP＝. 在△AOC与△BOP中. ①若∠OCA＝∠OBP.则△BOP∽△COA.∴. OP＝.∴. ②若∠OCA＝∠OPB.则△BOP∽△AOC.∴. .∴. ∴存在符合题意的点P.其坐标为或 中考零距离答案
网址：http://m.1010jiajiao.com/timu3_id_452746[举报]
如图，已知抛物线与x轴交于点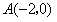
，
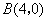，与y轴交于点
．
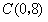（1）求抛物线的解析式及其顶点D的坐标；
（2）设直线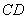
交x轴于点E．在线段
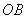的垂直平分线上是否存在点P，使得点P到直线
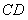的距离等于点P到原点O的距离？如果存在，求出点P的坐标；如果不存在，请说明理由；
（3）过点B作x轴的垂线，交直线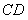
于点F，将抛物线沿其对称轴平移，使抛物线与线段
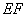总有公共点．试探究：抛物线向上最多可平移多少个单位长度？向下最多可平移多少个单位长度？
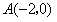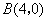，，与y轴交于点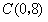．（1）求抛物线的解析式及其顶点D的坐标；
（2）设直线
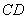交x轴于点E．在线段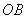的垂直平分线上是否存在点P，使得点P到直线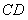的距离等于点P到原点O的距离？如果存在，求出点P的坐标；如果不存在，请说明理由；（3）过点B作x轴的垂线，交直线
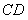于点F，将抛物线沿其对称轴平移，使抛物线与线段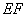总有公共点．试探究：抛物线向上最多可平移多少个单位长度？向下最多可平移多少个单位长度？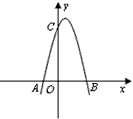 
已知点A（1，3），B（3，2）．（1）在如图所示边长为1的正方形网格中建立平面直角坐标系描出点A、B．
（2）求出△AOB的面积（其中O为坐标原点）
（3）设AB交x轴于点C，求C点的坐标．
（4）试在x轴上找一点D，使S△ADB=2S△AOB．
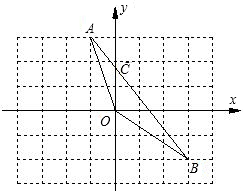如图，在直角坐标系中，A（-1，3），B（3，-2）．
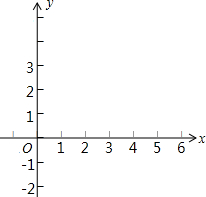已知平面直角坐标系中，A、B、C三点的坐标分别是（0，2）、（0，-2），（4，-2）．