摘要：2．(1)当点P运动2秒时.AP＝2cm.由∠A＝60°.知AE＝1.PE＝.∴. 当0≤t≤6时.点P与点Q都在AB上运动.设PM与AD交于点G.QN与AD交于点F.则AQ＝t.AF＝.QF＝.AP＝t+2.AG＝1+.PG＝. ∴此时两平行线截平行四边形ABCD的面积为. (ii)当6≤t≤8时.点P在BC上运动.点Q仍在AB上运动.设PM与DC交于点G.QN与AD交于点F.则AQ＝t.AF＝.DF＝4-.QF＝.BP＝t-6. CP＝10-t.PG＝. 而BD＝.故此时两平行线截平行四边形ABCD的面积为. (iii)当8≤t≤10时.点P和点Q都在BC上运动.设PM与DC交于点G.QN与DC交于点F.则CQ＝20-2t.OF＝.CP＝10-t.PG＝. ∴此时两平行线截平行四边形ABCD的面积为. 故S关于t的函数关系式为 ②当0≤t≤6时.S的最大值为, 当6≤t≤8时.S的最大值为. 当8≤t≤10时.S的最大值为 所以当t＝8时.S有最大值为.
网址：http://m.1010jiajiao.com/timu3_id_452744[举报]
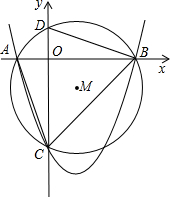如图，已知抛物线y=ax2+bx-3与x轴交于A、B两点，与y轴交于C点，经过A、B、C三点的圆的圆心M（1，m）恰好在此抛物线的对称轴上，⊙M的半径为| 5 |
（1）求m、a、b的值；
（2）若动点P从点C出发，沿线段CB以每秒2个单位长的速度运动，过点P作y轴的平行线交抛物线于Q．当点P运动几秒时，线段PQ的值最大，并求此时P点坐标；
（3）在（2）条件下，当线段PQ的值最大时，四边形ACQB面积是否也最大？说明理由．
等腰直角三角形ABC的直角边AB=BC=10cm，点P、Q分别从A、C两点同时出发，均以1cm/秒的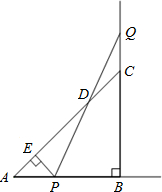
相同速度做直线运动，已知P沿射线AB运动，Q沿边BC的延长线运动，PQ与直线AC相交于D．
（1）当点P运动几秒时，△PCQ的面积等于△ABC的面积？
（2）作PE⊥AC于点E，当点P、Q运动时，线段DE的长度是否改变？证明你的结论． 查看习题详情和答案>>
相同速度做直线运动，已知P沿射线AB运动，Q沿边BC的延长线运动，PQ与直线AC相交于D．（1）当点P运动几秒时，△PCQ的面积等于△ABC的面积？
（2）作PE⊥AC于点E，当点P、Q运动时，线段DE的长度是否改变？证明你的结论． 查看习题详情和答案>>
已知：矩形OABC的顶点O在平面直角坐标系的原点，边OA、OC分别在x、y轴的正半轴 上，且OA=3cm，OC=4cm，点M从点A出发沿AB向终点B运动，点N从点C出发沿CA向终点A运动，点M、N同时出发，且运动的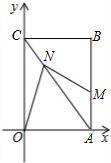
速度均为1cm/秒，当其中一个点到达终点时，另一点即停止运动．设运动的时间为t秒．
（1）当点N运动1秒时，求点N的坐标；
（2）试求出多边形OAMN的面积S与t的函数关系式；
（3）t为何值时，以△OAN的一边所在直线为对称轴翻折△OAN，翻折前后的两个三角形所组成的四边形为菱形？ 查看习题详情和答案>>
速度均为1cm/秒，当其中一个点到达终点时，另一点即停止运动．设运动的时间为t秒．（1）当点N运动1秒时，求点N的坐标；
（2）试求出多边形OAMN的面积S与t的函数关系式；
（3）t为何值时，以△OAN的一边所在直线为对称轴翻折△OAN，翻折前后的两个三角形所组成的四边形为菱形？ 查看习题详情和答案>>
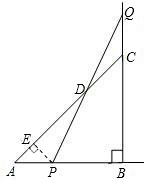等腰△ABC的直角边AB=BC=10cm，点P、Q分别从A、C两点同时出发，均以1cm/秒的相同速度作直线运动，已知P沿射线AB运动，Q沿边BC的延长线运动，PQ与直线AC相交于点D．设P点运动时间为t，△PCQ的面积为S．
速度在劣弧BC上运动，且运动时间为t（秒），∠AOB=90°、∠BOP=n°．