摘要：(1)设直线OM的函数关系式为． 则∴． ∴直线OM的函数关系式为． (2)∵的坐标满足.∴点在直线OM上． (或用几何证法.见教师用书191页) ∵四边形PQRM是矩形.∴SP=SQ=SR=SM=PR． ∴∠SQR=∠SRQ． ∵PR=2OP.∴PS=OP=PR．∴∠POS=∠PSO． ∵∠PSQ是△SQR的一个外角. ∴∠PSQ=2∠SQR．∴∠POS=2∠SQR． ∵QR∥OB.∴∠SOB=∠SQR． ∴∠POS=2∠SOB． ∴∠SOB=∠AOB． (3)以下方法只要回答一种即可． 方法一:利用钝角的一半是锐角.然后利用上述结论把锐角三等分的方法即可．
网址：http://m.1010jiajiao.com/timu3_id_452005[举报]
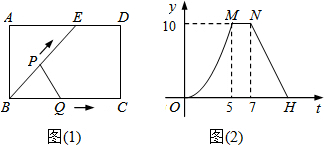
如图1，点E为矩形ABCD边AD上一点，点P，点Q同时从点B出发，点P沿BE→ED→DC运动到点C停止，点Q沿BC运动到点C停止，它们的运动速度都是1cm/s，设P，Q出发t秒时，△BPQ的面积为ycm2，已知y与t的函数关
系的图象如图2（曲线OM为抛物线的一部分），则下列结论：
①AD=BE=5cm；
②当0＜t≤5时，y=
t2；
③直线NH的解析式为y=-
t+27；
④若△ABE与△QBP相似，则t=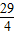
秒，
其中正确结论的个数为（ ）
A．4
B．3
C．2
D．1
查看习题详情和答案>>
系的图象如图2（曲线OM为抛物线的一部分），则下列结论：①AD=BE=5cm；
②当0＜t≤5时，y=
t2；③直线NH的解析式为y=-
t+27；④若△ABE与△QBP相似，则t=
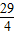秒，其中正确结论的个数为（ ）
A．4
B．3
C．2
D．1
查看习题详情和答案>>
如图1，点E为矩形ABCD边AD上一点，点P，点Q同时从点B出发，点P沿BE→ED→DC运动到点C停止，点Q沿BC运动到点C停止，它们的运动速度都是1cm/s，设P、Q出发t秒时，△BPQ的面积为y（cm2），已知y与t的函数关系的图象如图2（曲线OM为抛物线的一部分），则下列结论：
①AD=BE=5cm；
②当0＜t≤5时，y=
t2；
③直线NH的解析式为y=-
t+27；
④若△ABE与△QBP相似，则t=
秒，
其中正确结论的个数为（ ）
查看习题详情和答案>>
①AD=BE=5cm；
②当0＜t≤5时，y=
| 2 |
| 5 |
③直线NH的解析式为y=-
| 2 |
| 5 |
④若△ABE与△QBP相似，则t=
| 29 |
| 4 |
其中正确结论的个数为（ ）
| A．4 | B．3 | C．2 | D．1 |
（2013•南充）如图1，点E为矩形ABCD边AD上一点，点P，点Q同时从点B出发，点P沿BE→ED→DC运动到点C停止，点Q沿BC运动到点C停止，它们的运动速度都是1cm/s，设P，Q出发t秒时，△BPQ的面积为ycm2，已知y与t的函数关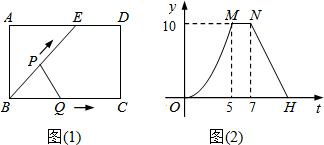
系的图象如图2（曲线OM为抛物线的一部分），则下列结论：
①AD=BE=5cm；
②当0＜t≤5时，y=
t2；
③直线NH的解析式为y=-
t+27；
④若△ABE与△QBP相似，则t=
秒，
其中正确结论的个数为（ ）
系的图象如图2（曲线OM为抛物线的一部分），则下列结论：①AD=BE=5cm；
②当0＜t≤5时，y=
| 2 |
| 5 |
③直线NH的解析式为y=-
| 2 |
| 5 |
④若△ABE与△QBP相似，则t=
| 29 |
| 4 |
其中正确结论的个数为（ ）
查看习题详情和答案>>
；③直线NH的解析式为
；④若△ABE与△QBP相似，则t=
秒。其中正确的结论个数为【 】
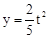；③直线NH的解析式为
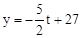；④若△ABE与△QBP相似，则t=
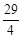秒。其中正确的结论个数为【 】