网址:http://m.1010jiajiao.com/timu3_id_452002[举报]
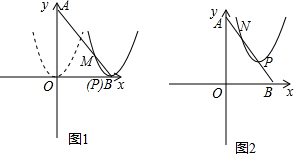
如图1,在平面直角坐标系中,点O是坐标原点,四边形ABCO是菱形,点A的坐标为(-3,4),点C在x轴的正半轴上,直线AC交y轴于点M,AB边交y轴于点H.
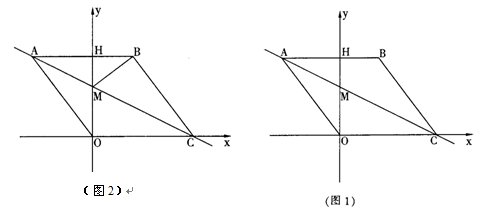
(1)求直线AC的解析式;
(2)连接BM,如图2,动点P从点A出发,沿折线ABC方向以2个单位/秒的速度向终点C匀速运动,设△PMB的面积为S(S≠0),点P的运动时间为t秒,求S与t之间的函数关系式(要求写出自变量t的取值范围);
(3)在(2)的条件下,当 t为何值时,∠MPB与∠BCO互为余角.
【解析】(1)已知A点的坐标,就可以求出OA的长,根据OA=OC,就可以得到C点的坐标,根据待定系数法就可以求出函数解析式.
(2)点P的位置应分P在AB和BC上,两种情况进行讨论.当P在AB上时,△PMB的底边PB可以用时间t表示出来,高是MH的长,因而面积就可以表示出来
(3)本题可以分:当P点在AB边上运动时,当P点在BC边上运动时,两种情况进行讨论,
查看习题详情和答案>>
如图1,在平面直角坐标系中,点O是坐标原点,四边形ABCO是菱形,点A的坐标为(-3,4),点C在x轴的正半轴上,直线AC交y轴于点M,AB边交y轴于点H.
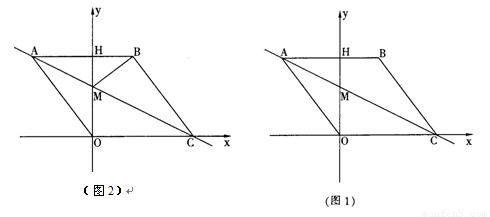
(1)求直线AC的解析式;
(2)连接BM,如图2,动点P从点A出发,沿折线ABC方向以2个单位/秒的速度向终点C匀速运动,设△PMB的面积为S(S≠0),点P的运动时间为t秒,求S与t之间的函数关系式(要求写出自变量t的取值范围);
(3)在(2)的条件下,当 t为何值时,∠MPB与∠BCO互为余角.
【解析】(1)已知A点的坐标,就可以求出OA的长,根据OA=OC,就可以得到C点的坐标,根据待定系数法就可以求出函数解析式.
(2)点P的位置应分P在AB和BC上,两种情况进行讨论.当P在AB上时,△PMB的底边PB可以用时间t表示出来,高是MH的长,因而面积就可以表示出来
(3)本题可以分:当P点在AB边上运动时,当P点在BC边上运动时,两种情况进行讨论,
查看习题详情和答案>>
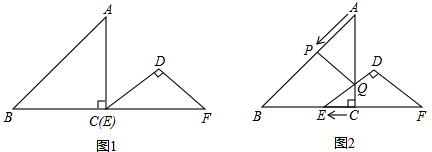
(1)当D在AC上时,求t的值;
(2)在P点运动过程中,是否存在点P,使△APQ为等腰三角形?若存在,求出t的值;若不存在,说明理由.
(3)连接PE,设四边形APEQ的面积为y(cm2),求y与t之间的函数关系式,并写出自变量t的取值范围.
| 3 | 4 |
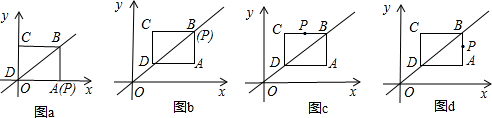
(1)求矩形ABCD周长;
(2)如图b,当P到达B时,求点P坐标;
(3)当点P在运动时,过点P作x轴、y轴的垂线,垂足分别为E、F,
①如图c,当P在BC上运动时,矩形PEOF的边能否与矩形ABCD的边对应成比例?若能,求出时间t的值,若不能,说明理由;
②如图d,当P在AB上运动时,矩形PEOF的面积能否等于256?若能,求出时间t的值,若不能,说明理由;
 查看习题详情和答案>>
查看习题详情和答案>>