摘要：(1) 在Rt△OAB中.∵∠AOB=30°.∴ OB=. 过点B作BD垂直于x轴.垂足为D.则 OD=.BD=.∴ 点B的坐标为() . (2) 将A(2,0).B().O(0,0)三点的坐标代入y=ax2+bx+c.得 解方程组.有 a=.b=.c=0. ∴ 所求二次函数解析式是 y=x2+x. (3) 设存在点C(x , x2+x) (其中0<x<).使四边形ABCO面积最大. ∵△OAB面积为定值. ∴只要△OBC面积最大.四边形ABCO面积就最大. 过点C作x轴的垂线CE.垂足为E.交OB于点F.则 S△OBC= S△OCF +S△BCF==. 而 |CF|=yC-yF=. ∴ S△OBC= . ∴ 当x=时.△OBC面积最大.最大面积为. 此时.点C坐标为().四边形ABCO的面积为.
网址：http://m.1010jiajiao.com/timu3_id_451993[举报]
（2008•宝安区二模）在Rt△OAB中，∠AOB=90°，已知AB=
，tan∠OAB=3，将△OAB绕点O按顺时针方向旋转90°得到△ODC，如图1建立坐标系．
（1）写出A、B、C三点坐标（不必写过程）；
（2）若抛物线y=ax2+bx+c经过A、B、C三点，如图2，M是抛物线的顶点，试判定△MCD的形状，并说明理由；
（3）在（2）的抛物线上，且在第一象限中，是否存在点P，使四边形BDCP的面积W最大？若存在，请求出这个最大面积；若不存在，请说明理由．
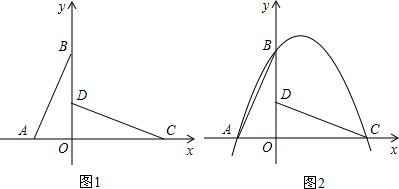
查看习题详情和答案>>
| 10 |
（1）写出A、B、C三点坐标（不必写过程）；
（2）若抛物线y=ax2+bx+c经过A、B、C三点，如图2，M是抛物线的顶点，试判定△MCD的形状，并说明理由；
（3）在（2）的抛物线上，且在第一象限中，是否存在点P，使四边形BDCP的面积W最大？若存在，请求出这个最大面积；若不存在，请说明理由．
（1）如图，在等腰梯形ABCD中，AD∥BC，M是AD的中点，求证：MB=MC．
（2）如图，在Rt△OAB中，∠OAB=90°，且点B的坐标为（4，2）．
①画出△OAB向下平移3个单位后的△O1A1B1；
②画出△OAB绕点O逆时针旋转90°后的△OA2B2，并求点A旋转到点A2所经过的路线长（结果保留π）． 查看习题详情和答案>>
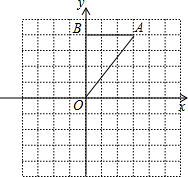如图，在Rt△OAB中，∠OBA=90°，且点B的坐标为（0，4）．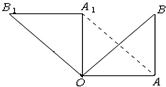
19、如图，在Rt△OAB中，∠OAB=90°，OA=AB=6，将△OAB绕点O沿逆时针方向旋转90°得到△OA1B1．