摘要:5.已知:在矩形ABCD中.AB=2.E为BC边上的一点.沿直线DE将矩形折叠.使C点落在AB边上的C点处.过C′作C′H⊥DC.C′H分别交DE.DC于点G.H.连结CG.CC′.CC′交GE于点F. (1) 求证:四边形CGC′’E为菱形, (2) 设.并设.试将表示成的函数, 中所求得的函数的图象达到最高点时.求BC的长 能力训练
网址:http://m.1010jiajiao.com/timu3_id_451904[举报]
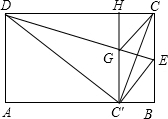 已知:在矩形ABCD中,AB=2,E为BC边上的一点,沿直线DE将矩形折叠,使C点落在AB边上的C点处.过C′作C′H⊥DC,C′H分别交DE、DC于点G、H,连接CG、CC′,CC′交GE于点F.
已知:在矩形ABCD中,AB=2,E为BC边上的一点,沿直线DE将矩形折叠,使C点落在AB边上的C点处.过C′作C′H⊥DC,C′H分别交DE、DC于点G、H,连接CG、CC′,CC′交GE于点F.(1)求证:四边形CGC′E为菱形;
(2)设sin∠CDE=x,并设y=
| C′E+DG | DE |
(3)当(2)中所求得的函数的图象达到最高点时,求BC的长. 查看习题详情和答案>>
已知:在矩形ABCD中,AB=10,BC=12,四边形EFGH的三个顶点E、F、H分别在矩形ABCD边AB、BC、DA上,AE=2.
(1)如图①,当四边形EFGH为正方形时,求△GFC的面积;
(2)如图②,当四边形EFGH为菱形,且BF=a时,求△GFC的面积(用a表示);
(3)在(2)的条件下,△GFC的面积能否等于2?请说明理由.
已知:在矩形ABCD中,AB=10,BC=12,四边形EFGH的三个顶点E、F、H分别在矩形ABCD边AB、BC、DA上,AE=2.
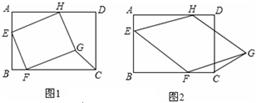
(1)如图①,当四边形EFGH为正方形时,求△GFC的面积;
(2)如图②,当四边形EFGH为菱形,且BF=a时,求△GFC的面积(用a表示);
(3)在(2)的条件下,△GFC的面积能否等于2?请说明理由.
查看习题详情和答案>>
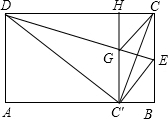 已知:在矩形ABCD中,AB=2,E为BC边上的一点,沿直线DE将矩形折叠,使C点落在AB边上的C点处.过C′作C′H⊥DC,C′H分别交DE、DC于点G、H,连接CG、CC′,CC′交GE于点F.
已知:在矩形ABCD中,AB=2,E为BC边上的一点,沿直线DE将矩形折叠,使C点落在AB边上的C点处.过C′作C′H⊥DC,C′H分别交DE、DC于点G、H,连接CG、CC′,CC′交GE于点F. ,试将y表示成x的函数;
,试将y表示成x的函数;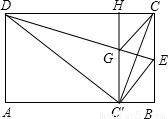 已知:在矩形ABCD中,AB=2,E为BC边上的一点,沿直线DE将矩形折叠,使C点落在AB边上的C点处.过C′作C′H⊥DC,C′H分别交DE、DC于点G、H,连接CG、CC′,CC′交GE于点F.
已知:在矩形ABCD中,AB=2,E为BC边上的一点,沿直线DE将矩形折叠,使C点落在AB边上的C点处.过C′作C′H⊥DC,C′H分别交DE、DC于点G、H,连接CG、CC′,CC′交GE于点F.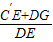 ,试将y表示成x的函数;
,试将y表示成x的函数;