Question

已知：在矩形ABCD中，AB＝10，BC＝12，四边形EFGH的三个顶点E、F、H分别在矩形ABCD边AB、BC、DA上，AE＝2．

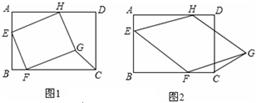
（1）如图①，当四边形EFGH为正方形时，求△GFC的面积；

（2）如图②，当四边形EFGH为菱形，且BF＝a时，求△GFC的面积（用a表示）；

（3）在（2）的条件下，△GFC的面积能否等于2？请说明理由．

 

Answer 1

【答案】

（1）10；（2）12－a；（3）不能

【解析】

试题分析：（1）过点G作GM⊥BC于M，根据正方形的性质及同角的余角相等可证得△AHE≌△BEF，同理可证：△MFG≌△BEF，即可得到GM＝BF＝AE＝2，再根据三角形的面积公式求解即可；

（2）过点G作GM⊥BC于M．连接HF，根据平行线的性质可得∠AHF＝∠MFH，∠EHF＝∠GFH，即得∠AHE＝∠MFG，再结合∠A＝∠GMF＝90°，EH＝GF可证得△AHE≌△MFG，即可得到GM＝AE＝2，再根据三角形的面积公式求解即可；

（3）若S_△GFC＝2，则12－a＝2，解得a＝10．此时在△BEF中，根据勾股定理求得EF的长，在△AHE中，根据勾股定理求得AH的长，由AH＞AD，即点H已经不在边AB上，故不可能有S_△GFC＝2．

（1）过点G作GM⊥BC于M

在正方形EFGH中，∠HEF＝90°，EH＝EF，

∴∠AEH+∠BEF＝90°，

∵∠AEH＋∠AHE＝90°，

∴∠AHE＝∠BEF，

又∵∠A＝∠B＝90°，

∴△AHE≌△BEF．

同理可证：△MFG≌△BEF，

∴GM＝BF＝AE＝2，

∴FC＝BC－BF＝10，

则S_△GFC＝10；

（2）过点G作GM⊥BC于M．连接HF

∵AD∥BC，

∴∠AHF＝∠MFH，

∵EH∥FG，

∴∠EHF＝∠GFH，

∴∠AHE＝∠MFG．

又∵∠A＝∠GMF＝90°，EH＝GF，

∴△AHE≌△MFG．

∴GM＝AE＝2．

∴S_△GFC＝FC?GM＝（12－a）×2＝12－a；

（3）△GFC的面积不能等于2．

∵若S_△GFC＝2，则12－a＝2，解得a＝10．

此时，在△BEF中，EF＝＝＝，

在△AHE中，AH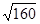＝＝＝＝＞12，

∴AH＞AD，即点H已经不在边AB上，故不可能有S_△GFC＝2．

考点：四边形的综合题

点评：此类问题综合性强，难度较大，在中考中比较常见，一般作为压轴题，题目比较典型．