摘要：21．已知:抛物线y=-x2+mx+2m2(m＞0)与x轴交于A.B两点.点A在点B的左边.C是抛物线上一个动点(点C与点A.B不重合).D是OC的中点.连结BD并延长.交AC于点E. (1)用含m的代数式表示点A.B的坐标, (2)求的值, (3)当C.A两点到y轴的距离相等.且时.求抛物线和直线BE的解析式.
网址：http://m.1010jiajiao.com/timu3_id_451716[举报]
已知：抛物线y＝x2＋mx＋n与x轴交A、B两点(A点在B点左侧)，B(3，0)，且经过C(2，－3)，与y轴交于点D，
(1)求此抛物线的解析式及顶点F的坐标；
(2)P是线段AC上的一个动点，过P点作y轴的平行线交抛物于E点，求线段PE长度的最大值；
(3)在(1)的条件下，在x轴上是否存在两个点G、H(G在H的左侧)，且GH＝2，使得线段GF＋FC＋CH＋HG的长度和为最小；如果存在，求出G、Ｈ的坐标；如果不存在，说明理由．
如图，已知：抛物线y＝x2＋bx－3与x轴相交于A、B两点，与y轴相交于点C，并且OA＝OC．
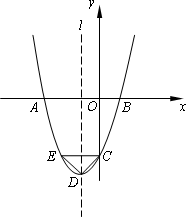
(1)求这条抛物线的解析式；
(2)过点C作CE∥x轴，交抛物线于点E，设抛物线的顶点为点D，试判断△CDE的形状，并说明理由；
(3)设点M在抛物线的对称轴l上，且△MCD的面积等于△CDE的面积，请写出点M的坐标(无需写出解题步骤)．
已知：抛物线y＝x2＋mx＋n与x轴交A、B两点(A点在B点左侧)，B(3，0)，
且经过C(2，－3)，与y轴交于点D，
(1)求此抛物线的解析式及顶点F的坐标；
(2)P是线段AC上的一个动点，过P点作y轴的平行线交抛物于E点，求线段PE长度的最大值；
(3)在(1)的条件下，在x轴上是否存在两个点G、H(G在H的左侧)，且GH＝2，使得线段GF＋FC＋CH＋HG的长度和为最小；如果存在，求出G、Ｈ的坐标；如果不存在，说明理由．
与抛物线y＝x2＋mx－
m2在平面直角坐标系xOy中的位置如图所示，其中一条与x轴交于A、B两点．
－
＝
，求经过A、B两点的这条抛物线的解析式．