摘要:如图13.在△ABC中.AB=AC.∠BAD=20°.且AE=AD.则∠CDE= . 图11 图12 图13
网址:http://m.1010jiajiao.com/timu3_id_451548[举报]
如图13,在![]() ABC中,∠BAC=90
ABC中,∠BAC=90![]() ,AB=AC,AB是
,AB=AC,AB是![]() O的直径,
O的直径,![]() O交BC于点D,DE
O交BC于点D,DE![]() AC于点E,BE交
AC于点E,BE交![]() O于点F,连接AF的延长线交DE于点P。
O于点F,连接AF的延长线交DE于点P。
(1)求证:DE是![]() O的切线。
O的切线。
(2)求tan∠ABE的值;
(3)若OA=2,求线段AP的长。

加试题(本小题满分20分,其中(1)、(2)、(3)题各3分,(4)题11分)
(1)一个正数的平方根为3-a和2a+3,则这个正数是
(2)若x2+2x+y2-6y+10=0,则xy=
(3)已知a,b分别是6-
的整数部分和小数部分,则2a-b=
(4)阅读下面的问题,并解答问题:
1)如图1,等边△ABC内有一点P,若点P到顶点A,B,C的距离分别为3,4,5,求∠APB的度数是多少?(请在下列横线上填上合适的答案)
分析:由于PA,PB,PC不在同一个三角形中,为了解决本题我们可以将△ABP绕顶点A逆时针旋转到△ACP′处,此时可以利用旋转的特征等知识得到:
①∠APB=∠AP′C=∠AP′P+∠PP′C;
②AP=AP′,且∠PAP′=
③P′C=BP=4,P′P=AP=3,PC=5,所以△PP′C为
2)请你利用第1)题的解答方法,完成下面问题:
如图2,在△ABC中,∠CAB=90°,AB=AC,E、F为边BC上的点,且∠EAF=45°,试说明:EF2=BE2+FC2.

查看习题详情和答案>>
(1)一个正数的平方根为3-a和2a+3,则这个正数是
81
81
(2)若x2+2x+y2-6y+10=0,则xy=
-1
-1
(3)已知a,b分别是6-
| 13 |
| 13 |
| 13 |
(4)阅读下面的问题,并解答问题:
1)如图1,等边△ABC内有一点P,若点P到顶点A,B,C的距离分别为3,4,5,求∠APB的度数是多少?(请在下列横线上填上合适的答案)
分析:由于PA,PB,PC不在同一个三角形中,为了解决本题我们可以将△ABP绕顶点A逆时针旋转到△ACP′处,此时可以利用旋转的特征等知识得到:
①∠APB=∠AP′C=∠AP′P+∠PP′C;
②AP=AP′,且∠PAP′=
60
60
度,所以△APP′为等边
等边
三角形,则∠AP′P=60
60
度;③P′C=BP=4,P′P=AP=3,PC=5,所以△PP′C为
直角
直角
三角形,则∠PP′C=90
90
度,从而得到∠APB=150
150
度.2)请你利用第1)题的解答方法,完成下面问题:
如图2,在△ABC中,∠CAB=90°,AB=AC,E、F为边BC上的点,且∠EAF=45°,试说明:EF2=BE2+FC2.

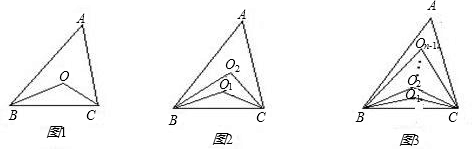
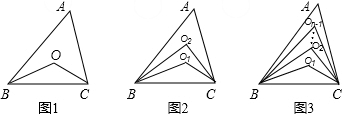
已知,如图1,在△ABC,∠ABC、∠ACB的角平分线交于点O,则∠BOC=90°+
∠A=
×180°+
∠A.如图2,在△ABC中,∠ABC、∠ACB的两条三等分角线分别对应交于O1、O2,则∠BO1C=
×180°+
∠A,∠BO2C=
×180°+
∠A.
根据以上阅读理解,你能猜想(n等分时,内部有n-1个点)(用n的代数式表示)
.
 查看习题详情和答案>>
查看习题详情和答案>>
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 2 |
| 3 |
根据以上阅读理解,你能猜想(n等分时,内部有n-1个点)(用n的代数式表示)
 查看习题详情和答案>>
查看习题详情和答案>>
如图1,在△ABC中,∠ABC,∠ACB的角平分线交于点O,则∠BOC=90°+
∠A=
×180°+
∠A.
如图2,在△ABC中,∠ABC,∠ACB的两条三等分角线分别对应交于O1,O2,则∠BO1C=
×180°+
∠A,∠BO2C=
×180°+
∠A.
根据以上阅读理解,你能猜想(n等分时,内部有n-1个点)(用n的代数式表示)∠BOn-1C=( )
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
如图2,在△ABC中,∠ABC,∠ACB的两条三等分角线分别对应交于O1,O2,则∠BO1C=
| 2 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 2 |
| 3 |
根据以上阅读理解,你能猜想(n等分时,内部有n-1个点)(用n的代数式表示)∠BOn-1C=( )

A、
| ||||
B、
| ||||
C、
| ||||
D、
|
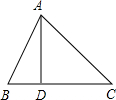 如图所示在△ABC中,AB=13,AD=12,AC=15,CD=9,求△ABC的面积.
如图所示在△ABC中,AB=13,AD=12,AC=15,CD=9,求△ABC的面积.