摘要:已知抛物线y=-x2+2(m-3)x+m-1与x轴交于B,A两点,其中点B在x轴的负半轴上,点A在x轴的正半轴上,该抛物线与y轴于点C. (1)写出抛物线的开口方向与点C的坐标, (2)若tg∠CBA=3,试求抛物线的解析式, 中抛物线上的一个动点,试求四边形AOCP的面积的最大值及此时点P的坐标. 附加题
网址:http://m.1010jiajiao.com/timu3_id_451129[举报]
已知抛物线y=x2+kx+k-2.
1.(1)求证:不论k为任何实数,抛物线与x轴总有两个交点;
2.(2)若反比例函数![]() 的图象与
的图象与![]() 的图象关于y轴对称,又与抛物线交于点A(n, -3),求抛物线的解析式;
的图象关于y轴对称,又与抛物线交于点A(n, -3),求抛物线的解析式;
3.(3)若点P是(2)中抛物线上的一点,且点P到两坐标轴的距离相等,求点P的坐标.
查看习题详情和答案>>
已知抛物线y=ax2+bx+c与直线y=mx+n相交于两点,这两点的坐标分别是(0,![]() )和(m-b,m2-mb+n),其中a,b,c,m,n为实数,且a,m不为0.
)和(m-b,m2-mb+n),其中a,b,c,m,n为实数,且a,m不为0.
(1)求c的值;
(2)设抛物线y=ax2+bx+c与x轴的两个交点是(x1,0)和(x2,0),求x1x2的值;
(3)当-1≤x≤1时,设抛物线y=ax2+bx+c上与x轴距离最大的点为P(xo,yo ),求这时|yo|的最小值.
查看习题详情和答案>>
已知抛物线y=ax2+bx+c与直线y=mx+n相交于两点,这两点的坐标分别是(0,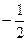 )和(m-b,m2-mb+n),其中a,b,c,m,n为实数,且a,m不为0.
)和(m-b,m2-mb+n),其中a,b,c,m,n为实数,且a,m不为0.
(1)求c的值;
(2)设抛物线y=ax2+bx+c与x轴的两个交点是(x1,0)和(x2,0),求x1x2的值;
(3)当-1≤x≤1时,设抛物线y=ax2+bx+c上与x轴距离最大的点为P(xo,yo ),求这时|yo|的最小值.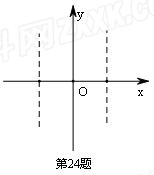 查看习题详情和答案>>
查看习题详情和答案>>
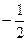 )和(m-b,m2-mb+n),其中a,b,c,m,n为实数,且a,m不为0.
)和(m-b,m2-mb+n),其中a,b,c,m,n为实数,且a,m不为0.(1)求c的值;
(2)设抛物线y=ax2+bx+c与x轴的两个交点是(x1,0)和(x2,0),求x1x2的值;
(3)当-1≤x≤1时,设抛物线y=ax2+bx+c上与x轴距离最大的点为P(xo,yo ),求这时|yo|的最小值.
 查看习题详情和答案>>
查看习题详情和答案>>
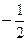 )和
)和 (m-b,m2-mb+n),其中a,b,c
(m-b,m2-mb+n),其中a,b,c ,m,n为实数,且a,m不为0.
,m,n为实数,且a,m不为0.