摘要:25.解:(1)...····················································· 2分 (2)分别过点作轴的垂线.垂足分别为. 分别过作于.于点. 在平行四边形中..又. . . 又. .·································································································· 5分 .. 设.由.得. 由.得..································ 7分 (此问解法多种.可参照评分) (3).或..························· 9分 (4)若为平行四边形的对角线.由(3)可得.要使在抛物线上. 则有.即. ..此时.································································ 10分 若为平行四边形的对角线.由(3)可得.同理可得.此时. 若为平行四边形的对角线.由(3)可得.同理可得.此时. 综上所述.当时.抛物线上存在点.使得以为顶点的四边形是平行四边形. 符合条件的点有... 12分 乐山市2007年28.如图(16).抛物线的图象与轴交于两点.与轴交于点.其中点的坐标为,直线与抛物线交于点.与轴交于点.且. (1)用表示点的坐标, (2)求实数的取值范围, (3)请问的面积是否有最大值? 若有.求出这个最大值,若没有.请说明理由.
网址:http://m.1010jiajiao.com/timu3_id_450912[举报]
如图,![]() 的顶点坐标分别为
的顶点坐标分别为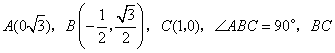 与
与![]() 轴的交点为
轴的交点为![]() 点坐标为
点坐标为 ,以点
,以点![]() 为顶点
为顶点![]() 轴为对称轴的抛物线过点
轴为对称轴的抛物线过点![]() .
.
(1)求该抛物线的解析式.
(2)将![]() 沿
沿![]() 折叠后得到点
折叠后得到点![]() 的对应点
的对应点![]() ,求证:四边形
,求证:四边形![]() 是矩形,并判断点
是矩形,并判断点![]() 是否在(1)的抛物线上.
是否在(1)的抛物线上.
(3)延长![]() 交抛物线于点
交抛物线于点![]() ,在线段
,在线段![]() 上取一点
上取一点![]() ,过点
,过点![]() 作
作![]() 轴的垂线,交抛物线于点
轴的垂线,交抛物线于点![]() ,是否存在这样的点
,是否存在这样的点![]() ,使四边形
,使四边形![]() 是平行四边形?若存在,求出点
是平行四边形?若存在,求出点![]() 的坐标,若不存在,说明理由.
的坐标,若不存在,说明理由.
 |
查看习题详情和答案>>
阅读下面问题:
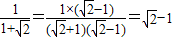 ;
;
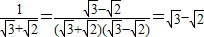 ;
;
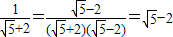 .
.
根据上面解法作出选择:已知Pn是反比例函数yn=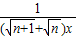 图象上的点(n=1、2、3…2009),分别过Pn做x轴的垂线,垂足是Mn.连接OPn,则这2009个直角三角形的面积和为( )
图象上的点(n=1、2、3…2009),分别过Pn做x轴的垂线,垂足是Mn.连接OPn,则这2009个直角三角形的面积和为( )
A.
B.
C.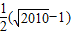
D.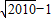
查看习题详情和答案>>
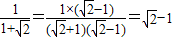 ;
;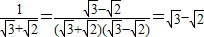 ;
;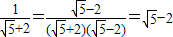 .
.根据上面解法作出选择:已知Pn是反比例函数yn=
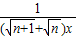 图象上的点(n=1、2、3…2009),分别过Pn做x轴的垂线,垂足是Mn.连接OPn,则这2009个直角三角形的面积和为( )
图象上的点(n=1、2、3…2009),分别过Pn做x轴的垂线,垂足是Mn.连接OPn,则这2009个直角三角形的面积和为( )A.

B.

C.
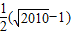
D.
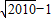
查看习题详情和答案>>
阅读下面问题:
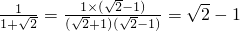 ;
;
 ;
;
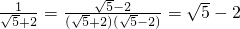 .
.
根据上面解法作出选择:已知Pn是反比例函数yn= 图象上的点(n=1、2、3…2009),分别过Pn做x轴的垂线,垂足是Mn.连接OPn,则这2009个直角三角形的面积和为
图象上的点(n=1、2、3…2009),分别过Pn做x轴的垂线,垂足是Mn.连接OPn,则这2009个直角三角形的面积和为
- A.

- B.

- C.

- D.

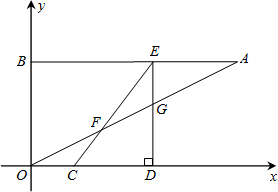
如图,A、B的坐标分别为(8,4),(0,4).点C从原点O出发以每秒1单位的速度沿着x轴的正方向运动,设运动时间为t(0<t<5).点D在x轴上,坐标为(t+3,0),过点D作x轴的垂线交AB于E点,交OA于G点,连接CE交OA于点F.
(1)填空:CD=______,CE=______,AE=______ (用含t的代数式表示);
(2)当△EFG的面积为 时,点G恰好在函数
时,点G恰好在函数 第一象限的图象上.试求出函数
第一象限的图象上.试求出函数 的解析式;
的解析式;
(3)设点Q的坐标为(0,2t),点P在(2)中的函数 的图象上,是否存在以A、C、Q、P为顶点的四边形是平行四边形?若存在,试求出点C、P的坐标;若不存在,请说明理由.
的图象上,是否存在以A、C、Q、P为顶点的四边形是平行四边形?若存在,试求出点C、P的坐标;若不存在,请说明理由.
查看习题详情和答案>>
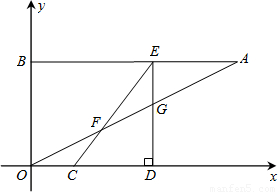
如图,A、B的坐标分别为(8,4),(0,4).点C从原点O出发以每秒1单位的速度沿着x轴的正方向运动,设运动时间为t(0<t<5).点D在x轴上,坐标为(t+3,0),过点D作x轴的垂线交AB于E点,交OA于G点,连接CE交OA于点F.
(1)填空:CD=______,CE=______,AE=______ (用含t的代数式表示);
(2)当△EFG的面积为 时,点G恰好在函数
时,点G恰好在函数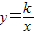 第一象限的图象上.试求出函数
第一象限的图象上.试求出函数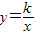 的解析式;
的解析式;
(3)设点Q的坐标为(0,2t),点P在(2)中的函数 的图象上,是否存在以A、C、Q、P为顶点的四边形是平行四边形?若存在,试求出点C、P的坐标;若不存在,请说明理由.
的图象上,是否存在以A、C、Q、P为顶点的四边形是平行四边形?若存在,试求出点C、P的坐标;若不存在,请说明理由.
查看习题详情和答案>>
(1)填空:CD=______,CE=______,AE=______ (用含t的代数式表示);
(2)当△EFG的面积为
 时,点G恰好在函数
时,点G恰好在函数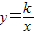 第一象限的图象上.试求出函数
第一象限的图象上.试求出函数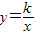 的解析式;
的解析式;(3)设点Q的坐标为(0,2t),点P在(2)中的函数
 的图象上,是否存在以A、C、Q、P为顶点的四边形是平行四边形?若存在,试求出点C、P的坐标;若不存在,请说明理由.
的图象上,是否存在以A、C、Q、P为顶点的四边形是平行四边形?若存在,试求出点C、P的坐标;若不存在,请说明理由.
查看习题详情和答案>>