题目内容
阅读下面问题:
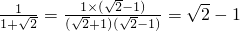 ;
;
 ;
;
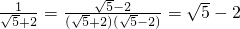 .
.
根据上面解法作出选择:已知Pn是反比例函数yn= 图象上的点(n=1、2、3…2009),分别过Pn做x轴的垂线,垂足是Mn.连接OPn,则这2009个直角三角形的面积和为
图象上的点(n=1、2、3…2009),分别过Pn做x轴的垂线,垂足是Mn.连接OPn,则这2009个直角三角形的面积和为
- A.

- B.

- C.

- D.

C
分析:根据反比例函数的比例系数k的几何意义,可知S△OPnMn= (
(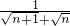 ),再令n=1,2,…,2009,将它们相加即可求出2009个直角三角形的面积和.
),再令n=1,2,…,2009,将它们相加即可求出2009个直角三角形的面积和.
解答:S△OP1M1+S△OP2M2+S△OP3M3+…+S△OP2009M2009
= (
( +
+ +
+ +…+
+…+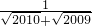 )
)
= (-1+
(-1+ -
- +
+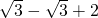 +…
+…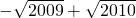 )
)
= .
.
故选C.
点评:本题主要考查反比例函数的比例系数k与其图象上的点与原点所连的线段、坐标轴、向坐标轴作垂线所围成的直角三角形面积S的关系,即S= |k|.
|k|.
分析:根据反比例函数的比例系数k的几何意义,可知S△OPnMn=
 (
(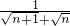 ),再令n=1,2,…,2009,将它们相加即可求出2009个直角三角形的面积和.
),再令n=1,2,…,2009,将它们相加即可求出2009个直角三角形的面积和.解答:S△OP1M1+S△OP2M2+S△OP3M3+…+S△OP2009M2009
=
 (
( +
+ +
+ +…+
+…+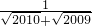 )
)=
 (-1+
(-1+ -
- +
+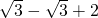 +…
+…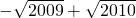 )
)=
 .
.故选C.
点评:本题主要考查反比例函数的比例系数k与其图象上的点与原点所连的线段、坐标轴、向坐标轴作垂线所围成的直角三角形面积S的关系,即S=
 |k|.
|k|. 
练习册系列答案
 启东小题作业本系列答案
启东小题作业本系列答案
相关题目