摘要:当y=360时.50x-150=360.解得x=10.2. 所以S=50×10.2+100=610. 答:需售门票 920张或 1020张.相应地需支付成本费用分别为56000元或 61000元. 点拨:正确理解题意.注意单位的统一. [例4]如图2-1-4所示.A.B两个旅游点从2001年至2005年“五.一 的旅游人数变化情况分别用实线和虚线表示.根据图中所示解答以下问题: (1)B旅游点的旅游人数相对上一年.增长最快的是哪一年? (2)求A.B两个旅游点从2001到2005年旅游人数的平均数和方差.并从平均数和方差的角度.用一句话对这两个旅游点的情况进行评价, (3)A旅游点现在的门票价格为每人80元.为保护旅游点环境和游客的安全.A旅游点的最佳接待人 数为4万人.为控制游客数量.A旅游点决定提高门票价格.已知门票价格x(元)与游客人数y满足函数关系.若要使A旅游点的游客人数不超过4万人.则门票价格至少应提高多少? 解:(1)B旅游点的旅游人数相对上一年增长最快的是2004年. (2)==3 ==3 = [(-2)+(-1)+0+1+2]=2 =[0+0+(-1)+1+0]= 从2001至2005年.A.B两个旅游点平均每年的旅游人数均为3万人.但A旅游点较B旅游点的旅游人数波动大. (3)由题意.得5-≤4, 解得x≥100. 100-80=20 答:A旅游点的门票至少要提高20元. Ⅲ.综合巩固练习:
网址:http://m.1010jiajiao.com/timu3_id_450619[举报]
如图,点A、B在直线l上,AB=24cm,⊙A、⊙B的半径开始都为2cm,⊙A以2cm/s的速度自左向右运动,设运动时间为t(s),
自⊙A开始运动时,⊙B的半径不断增大,其半径r(cm)与时间t之间的关系式为r=2+t.

(1)写出点A、B之间的距离y(cm)与时间t之间的函数关系式;
(2)⊙A出发后多少秒两圆相切?
(3)当t=4时,⊙A停止向右运动,与此同时,⊙B的半径也不再增大,记直线l与⊙B左侧的交点为点C,将⊙A绕点C在平面内旋转360°.问:⊙A与⊙B能否相切?若能,请直接写出相切几次;若不能,请说明理由. 查看习题详情和答案>>
自⊙A开始运动时,⊙B的半径不断增大,其半径r(cm)与时间t之间的关系式为r=2+t.

(1)写出点A、B之间的距离y(cm)与时间t之间的函数关系式;
(2)⊙A出发后多少秒两圆相切?
(3)当t=4时,⊙A停止向右运动,与此同时,⊙B的半径也不再增大,记直线l与⊙B左侧的交点为点C,将⊙A绕点C在平面内旋转360°.问:⊙A与⊙B能否相切?若能,请直接写出相切几次;若不能,请说明理由. 查看习题详情和答案>>
 某通讯公司推出了移动电话的两种计费方式(详情表1).
某通讯公司推出了移动电话的两种计费方式(详情表1).设一个月内使用移动电话主叫的时间为t分(t为正整数),请根据表1中提供的信息回答下列问题:
| 月使用 费/元 |
主叫限定时间/分 | 主叫超时费/(元/分) | 被叫 | |
| 方式一 | 58 | 150 | 0.25 | 免费 |
| 方式二 | 88 | 350 | 0.19 | 免费 |
(Ⅰ)用含有t的式子填写表2:
| t≤150 | 150<t<350 | t=350 | t>350 | |
| 方式一计费/元 | 58 | 108 | ||
| 方式二计费/元 | 88 | 88 | 88 |
(Ⅱ)t=360时,你认为选用哪种计费方式省钱;
(Ⅲ)当t为何值时,两种计费方式的费用相等.
阅读材料并解答问题:
与正三角形各边都相切的圆叫做正三角形的内切圆,与正四边形各边都相切的圆叫做正四边形的内切圆,与正n边形各边都相切的圆叫做正n边形的内切圆,设正n(n≥3)边形的面积为S正n边形,其内切圆的半径为r,试探索正n边形的面积.
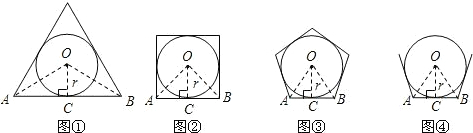
(1)如图1,当n=3时,设AB切⊙P于点C,连接OC,OA,OB,
∴OC⊥AB,
∴OA=OB,
∴∠AOC=
∠AOB,∴AB=2BC.
在Rt△AOC中,
∵∠AOC=
•
=60°,OC=r,
∴AC=r•tan60°,∴AB=2r•tan60°,
∴S△OAB=
•r•2r•tan60°=r2tan60°,
∴S正三角形=3S△OAB=3r2•tan60度.
(2)如图2,当n=4时,仿照(1)中的方法和过程可求得:S正四边形=4S△OAB= ;
(3)如图3,当n=5时,仿照(1)中的方法和过程求S正五边形;
(4)如图4,根据以上探索过程,请直接写出S正n边形= .
查看习题详情和答案>>
与正三角形各边都相切的圆叫做正三角形的内切圆,与正四边形各边都相切的圆叫做正四边形的内切圆,与正n边形各边都相切的圆叫做正n边形的内切圆,设正n(n≥3)边形的面积为S正n边形,其内切圆的半径为r,试探索正n边形的面积.

(1)如图1,当n=3时,设AB切⊙P于点C,连接OC,OA,OB,
∴OC⊥AB,
∴OA=OB,
∴∠AOC=
| 1 |
| 2 |
在Rt△AOC中,
∵∠AOC=
| 1 |
| 2 |
| 360° |
| 3 |
∴AC=r•tan60°,∴AB=2r•tan60°,
∴S△OAB=
| 1 |
| 2 |
∴S正三角形=3S△OAB=3r2•tan60度.
(2)如图2,当n=4时,仿照(1)中的方法和过程可求得:S正四边形=4S△OAB=
(3)如图3,当n=5时,仿照(1)中的方法和过程求S正五边形;
(4)如图4,根据以上探索过程,请直接写出S正n边形=
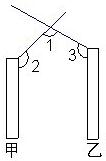 16、如图,甲、乙两栋平行的大楼顶部各有一个射灯,当光柱相交时,则∠1+∠2+∠3=
16、如图,甲、乙两栋平行的大楼顶部各有一个射灯,当光柱相交时,则∠1+∠2+∠3= 4、如图,平行的两幢大楼顶部各有一个射灯,当光柱相交时,∠1+∠2+∠3等于( )
4、如图,平行的两幢大楼顶部各有一个射灯,当光柱相交时,∠1+∠2+∠3等于( )