摘要:正比例函数和一次函数是分别用和来定义的.其中是自变量.是自变量的函数.k是自变量的系数.是常数.这两种函数解析式都是方程.而且它的图象上的点的坐标都是对应方程的解.因此.一次函数与一次方程有密不可分的关系.
网址:http://m.1010jiajiao.com/timu3_id_450400[举报]
有四张卡片(形状、大小和质地都相同),正面分别写有字母A、B、C、D和一个坐标,将这四张卡片背面向上洗匀,从中随机先抽取一张(不放回),接着再随机抽取一张.

(1)求出第一次抽出的卡片上的坐标是在第一象限的概率.
(2)用画树状图或列表法表示抽取两张卡片上的坐标都在反比例函数y=
图象上的概率.(卡片可用A、B、C、D表示)
查看习题详情和答案>>

(1)求出第一次抽出的卡片上的坐标是在第一象限的概率.
(2)用画树状图或列表法表示抽取两张卡片上的坐标都在反比例函数y=
| 3 | x |
有四张卡片(形状、大小和质地都相同),正面分别写有字母A、B、C、D和一个坐标,将这四张卡片背面向上洗匀,从中随机先抽取一张(不放回),接着再随机抽取一张.

(1)求出第一次抽出的卡片上的坐标是在第一象限的概率.
(2)用画树状图或列表法表示抽取两张卡片上的坐标都在反比例函数 图象上的概率.(卡片可用A、B、C、D表示)
图象上的概率.(卡片可用A、B、C、D表示)
查看习题详情和答案>>
有四张卡片(形状、大小和质地都相同),正面分别写有字母A、B、C、D和一个坐标,将这四张卡片背面向上洗匀,从中随机先抽取一张(不放回),接着再随机抽取一张.

(1)求出第一次抽出的卡片上的坐标是在第一象限的概率.
(2)用画树状图或列表法表示抽取两张卡片上的坐标都在反比例函数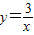 图象上的概率.(卡片可用A、B、C、D表示)
图象上的概率.(卡片可用A、B、C、D表示)
查看习题详情和答案>>

(1)求出第一次抽出的卡片上的坐标是在第一象限的概率.
(2)用画树状图或列表法表示抽取两张卡片上的坐标都在反比例函数
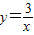 图象上的概率.(卡片可用A、B、C、D表示)
图象上的概率.(卡片可用A、B、C、D表示)查看习题详情和答案>>
通过对苏科版八(下)教材一道习题的探索研究,我们知道:一次函数y=x-1的图象可以由正比例函数y=x的图象向右平移1个单位长度得到类似的,函数y=
(k≠0)的图象是由反比例函数y=
(k≠0)的图象向左平移2个单位长度得到.灵活运用这一知识解决问题.
如图,已知反比例函数y=
的图象C与正比例函数y=ax(a≠0)的图象l相交于点A(2,2)和点B.
(1)写出点B的坐标,并求a的值;
(2)将函数y=
的图象和直线AB同时向右平移n(n>0)个单位长度,得到的图象分别记为C′和l′,已知图象C′经过点M(2,4).
①求n的值;
②分别写出平移后的两个图象C′和l′对应的函数关系式;
③直接写出不等式
≤ax-1的解集.

查看习题详情和答案>>
| k |
| x+2 |
| k |
| x |
如图,已知反比例函数y=
| 4 |
| x |
(1)写出点B的坐标,并求a的值;
(2)将函数y=
| 4 |
| x |
①求n的值;
②分别写出平移后的两个图象C′和l′对应的函数关系式;
③直接写出不等式
| 4 |
| x-1 |

 (2013•镇江)通过对苏科版八(下)教材一道习题的探索研究,我们知道:一次函数y=x-1的图象可以由正比例函数y=x的图象向右平移1个单位长度得到类似的,函数y=
(2013•镇江)通过对苏科版八(下)教材一道习题的探索研究,我们知道:一次函数y=x-1的图象可以由正比例函数y=x的图象向右平移1个单位长度得到类似的,函数y=| k |
| x+2 |
| k |
| x |
如图,已知反比例函数y=
| 4 |
| x |
(1)写出点B的坐标,并求a的值;
(2)将函数y=
| 4 |
| x |
①求n的值;
②分别写出平移后的两个图象C′和l′对应的函数关系式;
③直接写出不等式
| 4 |
| x-1 |