摘要：(二)证明题: 1.略 2.连结AB,BD,由射影定理得CD2=AC·CB,再证△BCF∽△APC. 3.(1)连结OD,则OD⊥DE,△OBD是等腰三角形,∠OBD=∠ODB=∠C,∴OD∥AC,∴OD⊥AC. (2)由切割线定理得ED2=BE·EF,连结AD,由射影定理得DE2=AE·EC,∴AE·EC=BE·EF. 4.△ACP∽△BAP ∴ 5.(1)△ACB和△CDB都Rt△ ∴∠CAD=∠BCD=∠EDB ∴DE∥AC (2)△ACD∽△CDF ∴. 6.设BP=,AP=,由割线定理得: ∵BH=2BC∴2BC2= .由△ABH∽△AHP ∴ ∴ 7.连结O,E交AB于F ∵∠1=∠2 ∴AE=BE,则O1E⊥AB,O1E平分AB ∴AB=2AF且∠AFE=Rt∠ △AEF≌△AEH AH=AF ∴AB=2AH (5)∵∠FAE= ∴ 8.∵AE,BD是方程的根,AE+BD=,∠BED=∠A+∠APE,∠BDE=∠DAP+∠BPE ∴∠BDE=∠BED BD=BE ∴AE+BE= ∴AB= AB是直径. (3) △ABP是Rt△, ∴ 由(1)题结论 ∴ ∴, BD= ∴
网址：http://m.1010jiajiao.com/timu3_id_450247[举报]
（1）如图，已知△ABC中，AB=4，BC=5，AC=3，AD、AE分别是BC边上的中线和高，求△A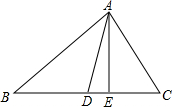
DE各边的长．
（2）通过上题的提示，你能够用同样方法证明的结论是（ ）
A、直角三角形中，30°角所对的边是斜边的一半．
B、直角三角形斜边上的中线等于斜边的一半．
C、Rt△ABC中，AE2=BE•CE．
查看习题详情和答案>>
DE各边的长．（2）通过上题的提示，你能够用同样方法证明的结论是（ ）
A、直角三角形中，30°角所对的边是斜边的一半．
B、直角三角形斜边上的中线等于斜边的一半．
C、Rt△ABC中，AE2=BE•CE．
证明题：说明理由(7分)如图，已知BE⊥AC于E，CF⊥AB于F，BE、CF相交于点D，若BD=CD.求证：AD平分∠BAC.
证明：∵BE⊥AC于E，CF⊥AB于F
∴∠BFD=∠CED=90°
又∵∠BDF=∠CDE( ) BD=CD
∴△BDF≌△CDE( )
∴DF=DE( )
∴AD平分∠BAC( ). 查看习题详情和答案>>
证明：∵BE⊥AC于E，CF⊥AB于F
∴∠BFD=∠CED=90°
又∵∠BDF=∠CDE( ) BD=CD
∴△BDF≌△CDE( )
∴DF=DE( )
∴AD平分∠BAC( ). 查看习题详情和答案>>
证明题：（1）等腰梯形的对角线交点与同一底的两个端点的距离相等．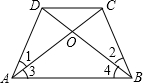
已知：如图，等腰梯形ABCD，BC=AD，两对角线相交于O点．
求证：OA=OB．
证明：∵在△ACD与△BDC中
BC=AD（______）
∠ADC=∠BCD（______）
______（公共边）
∴△ACD≌△BDC（______）
∴∠1=∠2 （______）
又∵∠DAB=∠ABC（等腰梯形的性质）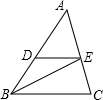
∴∠DAB-∠1=∠ABC-∠2
即：∠3=∠4（______）
∴______（ 等角对等边）
（2）已知：如图，△ABC中BE为∠B的角平分线DE∥BC．求证：BD=DE．
查看习题详情和答案>>
已知四边形ABCD的对角线AC与BD交于点O，给出下列四个论断
① OA=OC ② AB=CD ③ ∠BAD=∠DCB ④ AD∥BC
请你从中选择两个论断作为条件，以“四边形ABCD为平行四边形”作为结论，完成下列各题：
（1）构造一个真命题，画图并给出证明；
（2）构造一个假命题，举反例加以说明.
查看习题详情和答案>>
① OA=OC ② AB=CD ③ ∠BAD=∠DCB ④ AD∥BC
请你从中选择两个论断作为条件，以“四边形ABCD为平行四边形”作为结论，完成下列各题：
（1）构造一个真命题，画图并给出证明；
（2）构造一个假命题，举反例加以说明.
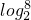log=3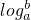（即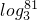
（即
（即