网址：http://m.1010jiajiao.com/timu3_id_450186[举报]
当
a＞0时：①抛物线y＝ax2＋bx＋c开口向________；②对称轴是直线________，顶点坐标为________；③在对称轴的左侧(即________)，y随x的增大而________，在对称轴的右侧(即________)，y随x的增大而________；④抛物线与对称轴的交点是抛物线的最低点，当x＝________时，y最小＝________．当
a＜0时：①抛物线y＝ax2＋bx＋c开口向________；②对称轴是直线________，顶点坐标为________；③在对称轴的左侧(即________)，y随x的增大而________，在对称轴的右侧(即________)，y随x的增大而________；④抛物线与对称轴的交点是抛物线的最高点，当x＝________时，y最大＝________．解：（1）A（-1，0），B（3，0），C（0，3）．·················· 2分
抛物线的对称轴是：x=1．······················· 3分
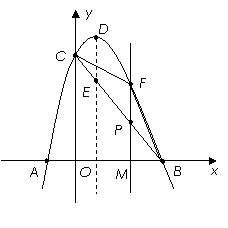（2）①设直线BC的函数关系式为：y=kx+b．
把B（3，0），C（0，3）分别代入得：
解得：k= -1，b=3．
所以直线BC的函数关系式为：
．
当x=1时，y= -1+3=2，∴E（1，2）．
当
时，
，
∴P（m，
m+3）．·························· 4分
在
中，当
时，
∴
当时，
∴
········· 5分
∴线段DE=4-2=2，线段
···· 6分
∵
∴当
时，四边形
为平行四边形．
由
解得：
（不合题意，舍去）．
因此，当
时，四边形为平行四边形．··········· 7分
②设直线
与
轴交于点
，由
可得：
∵
························ 8分
即
．
·········· 9分
（1）如图①．连接AC，将△OAC沿直线AC翻折，若点O的对应点0'恰好落在该抛物线的对称轴上，求实数a的值；
（2）如图②，在正方形EFGH中，点E、F的坐标分别是(4，4)、(4，3)，边HG位于边EF的右侧．小林同学经过探索后发现了一个正确的命题：“若点P是边EH或边HG上的任意一点，则四条线段PA、PB、PC、PD不能与任何一个平行四边形的四条边对应相等(即这四条线段不能构成平行四边形)．“若点P是边EF或边FG上的任意一点，刚才的结论是否也成立？请你积极探索，并写出探索过程；
（3）如图②，当点P在抛物线对称轴上时，设点P的纵坐标l是大于3的常数，试问：是否存在一个正数a，使得四条线段PA、PB、PC、PD与一个平行四边形的四条边对应相等(即这四条线段能构成平行四边形)？请说明理由． 查看习题详情和答案>>
巳知二次函数y＝a(x2－6x＋8)(a＞0)的图象与x轴分别交于点A、B，与y轴交于点C．点D是抛物线的顶点．
（1）如图①．连接AC，将△OAC沿直线AC翻折，若点O的对应点0'恰好落在该抛物线的对称轴上，求实数a的值；
（2）如图②，在正方形EFGH中，点E、F的坐标分别是(4，4)、(4，3)，边HG位于边EF的右侧．小林同学经过探索后发现了一个正确的命题：“若点P是边EH或边HG上的任意一点，则四条线段PA、PB、PC、PD不能与任何一个平行四边形的四条边对应相等(即这四条线段不能构成平行四边形)．“若点P是边EF或边FG上的任意一点，刚才的结论是否也成立？请你积极探索，并写出探索过程；
（3）如图②，当点P在抛物线对称轴上时，设点P的纵坐标l是大于3的常数，试问：是否存在一个正数a，使得四条线段PA、PB、PC、PD与一个平行四边形的四条边对应相等(即这四条线段能构成平行四边形)？请说明理由．