摘要：27． 某“研究性学习小组 遇到了以下问题.请参与: 已知.△ABC是等边三角形且内接于⊙O.取弧AB上异于A.B的点M．设直线CA与BM相交于点K.直线CB与AM相交于点N． (1)如图1.图2.图3.M分别为弧AB的中点.三分之一点.四分之一点.△ABC的边长均为2.分别测量出AK.BN的长.计算AK·BN的值并将结果填入下表中: △ABC的边长 AK·BN的值 图1 2 图2 2 图3 2 (2)如图4.当M为弧AB上任意一点时.根据(1)的结果.猜想AK·BN与AB的数量关系式为 , 中提出的猜想.依图4给出证明．
网址：http://m.1010jiajiao.com/timu3_id_450153[举报]
某研究性学习小组在探究矩形的折纸问题时，将一块直角三角板的直角顶点绕着矩形ABCD（AB＜BC）的对角线交点O旋转（如图①→②→③），图中M、N分别为直角三角板的直角边与矩形ABCD的边CD、BC的交点．
（1）该学习小组中一名成员意外地发现：在图①（三角板的一直角边与OD重合）中，BN2=CD2+CN2；在图③（三角板的一直角边与OC重合）中，CN2=BN2+CD2．请你对这名成员在图①和图③中发现的结论选择其一说明理由．
（2）试探究图②中BN、CN、CM、DM这四条线段之间的关系，写出你的结论，并说明理由．
查看习题详情和答案>>
（1）该学习小组中一名成员意外地发现：在图①（三角板的一直角边与OD重合）中，BN2=CD2+CN2；在图③（三角板的一直角边与OC重合）中，CN2=BN2+CD2．请你对这名成员在图①和图③中发现的结论选择其一说明理由．
（2）试探究图②中BN、CN、CM、DM这四条线段之间的关系，写出你的结论，并说明理由．
某研究性学习小组在探究矩形的折纸问题时，将一块直角三角板的直角顶点绕着矩形ABCD（DC＜BC）的对角线交点O旋转（如图①→②），图中M、N分别为直角三角板的直角边与三角形DBC的边CD、BC的交点．
（1）在图①（三角板的一直角边与OD重合）中，有CN2+DC2=BN2成立，请说明理由．
（2）试探究图②中BN、CN、CM、DM这四条线段之间的数量关系，请你用一个等式在横线上直接表示出探究的结论：
查看习题详情和答案>>
（1）在图①（三角板的一直角边与OD重合）中，有CN2+DC2=BN2成立，请说明理由．
（2）试探究图②中BN、CN、CM、DM这四条线段之间的数量关系，请你用一个等式在横线上直接表示出探究的结论：
CN2+CM2=DM2+BN2
CN2+CM2=DM2+BN2
．证明你的结论．
14、某研究性学习小组，为了了解本校八年级学生一天中做家庭作业所用的大致时间（时间以整数记，单位：分钟），对本年级同学做了抽样调查，并整理绘制成直方图如图所示．请按图中提供的信息回答下列问题．
（1）所抽取的样本容量是多少？
（2）在被调查的学生中，一天做家庭作业所用的大致时间超过120分钟的人数占被调查学生总人数的百分之几？
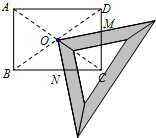某研究性学习小组在探究矩形的折纸问题时，将一块直角三角板的直角顶点绕着矩形ABCD的对角线交点O旋转（如图所示）．已知AB=8，BC=10，图中M、N分别为直角三角板的直角边与矩形ABCD的边CD、BC的交点．问：是否存在某一旋转位置，使得CM+CN等于
分成五个时间段，绘制成统计图（如图所示），请结合统计图中提供的信息，回答下列问题：