题目内容
14、某研究性学习小组，为了了解本校八年级学生一天中做家庭作业所用的大致时间（时间以整数记，单位：分钟），对本年级同学做了抽样调查，并整理绘制成直方图如图所示．请按图中提供的信息回答下列问题．
（1）所抽取的样本容量是多少？
（2）在被调查的学生中，一天做家庭作业所用的大致时间超过120分钟的人数占被调查学生总人数的百分之几？
分析：（1）根据直方图，将各组的频数相加可得答案；
（2）读图可知：一天做家庭作业所用的大致时间超过120分钟的人数有9+8+4=21人，再除以总人数即可得占被调查学生总人数的百分比．
（2）读图可知：一天做家庭作业所用的大致时间超过120分钟的人数有9+8+4=21人，再除以总人数即可得占被调查学生总人数的百分比．
解答：解：
（1）根据直方图可知，所抽取的样本容量是3+6+9+8+4=30；
答：所抽取的样本容量是30．
（2）读图可知：一天做家庭作业所用的大致时间超过120分钟的人数有9+8+4=21人，总人数为30人，
故有（9+8+4）÷30=70%．
答：一天做家庭作业所用的大致时间超过120分钟的人数占被调查学生总人数的70%．
（1）根据直方图可知，所抽取的样本容量是3+6+9+8+4=30；
答：所抽取的样本容量是30．
（2）读图可知：一天做家庭作业所用的大致时间超过120分钟的人数有9+8+4=21人，总人数为30人，
故有（9+8+4）÷30=70%．
答：一天做家庭作业所用的大致时间超过120分钟的人数占被调查学生总人数的70%．
点评：本题考查条形统计图、图表等知识．结合生活实际，绘制条形统计图或从统计图中获取有用的信息，是近年中考的热点．只要能认真准确读图，并作简单的计算，一般难度不大；注意：样本容量是指样本的具体数量，不带单位．
练习册系列答案
暑假作业海燕出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案
相关题目
某“研究性学习小组”遇到了以下问题，请参与：
已知，△ABC是等边三角形且内接于⊙O，取
上异于A、B的点M．设直线CA与BM相交于点K，直线CB与AM相交于点N．
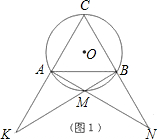
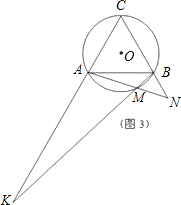
（1）如图1，图2，图3，M分别为
的中点、三分之一点、四分之一点，△ABC的边长均为2，分别测量出AK、BN的长，计算AK•BN的值（精确到0.01）并将结果填入下表中：
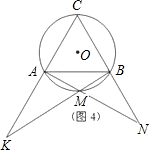
（2）如图4，当M为
上任意一点时，根据（1）的结果，猜想AK•BN与AB的数量关系式为 ；
（3）对（2）中提出的猜想，依图4给出证明．
已知，△ABC是等边三角形且内接于⊙O，取
 |
| AB |
（1）如图1，图2，图3，M分别为
|
| AB |
| △ABC的边长 | AK•BN的值 | |
| 图1 | 2 | |
| 图2 | 2 | |
| 图3 | 2 |
|
| AB |
（3）对（2）中提出的猜想，依图4给出证明．
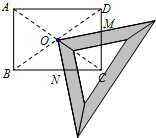某研究性学习小组在探究矩形的折纸问题时，将一块直角三角板的直角顶点绕着矩形ABCD的对角线交点O旋转（如图所示）．已知AB=8，BC=10，图中M、N分别为直角三角板的直角边与矩形ABCD的边CD、BC的交点．问：是否存在某一旋转位置，使得CM+CN等于
