摘要:若A是锐角.则= .
网址:http://m.1010jiajiao.com/timu3_id_449588[举报]
如图,△![]() 内接于⊙
内接于⊙![]() ,点
,点![]() 在
在![]() 的延长线上,sinB=
的延长线上,sinB=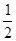 ,∠CAD=30°⑴求证:
,∠CAD=30°⑴求证: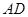 是⊙
是⊙![]() 的切线;⑵若
的切线;⑵若![]() ,求
,求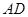 的长。
的长。
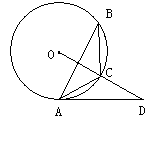
【解析】(1)连接OA,由于sinB=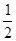 ,那么可求∠B=30°,利用圆周角定理可求∠AOC=60°,而OA=OB,那么△AOC是等边三角形,从而有∠OAC=60°,易求∠OAD=90°,即AD是⊙O的切线;
,那么可求∠B=30°,利用圆周角定理可求∠AOC=60°,而OA=OB,那么△AOC是等边三角形,从而有∠OAC=60°,易求∠OAD=90°,即AD是⊙O的切线;
(2)由于OC⊥AB,OC是半径,利用垂径定理可知OC是AB的垂直平分线,那么CA=CB,而∠B=30°,则∠BAC=30°,于是有∠DAE=60°,∠D=30°,在Rt△ACE中,利用三角函数值可求AE,在Rt△ADE中利用30°的锐角所对的直角边等于斜边的一半,可求AD.
查看习题详情和答案>>
如图,△ 内接于⊙
内接于⊙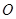 ,点
,点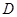 在
在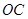 的延长线上,sinB=
的延长线上,sinB=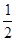 ,∠CAD=30°⑴求证:
,∠CAD=30°⑴求证: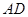 是⊙
是⊙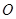 的切线;⑵若
的切线;⑵若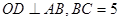 ,求
,求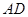 的长。
的长。
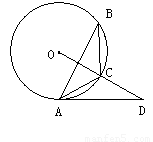
【解析】(1)连接OA,由于sinB=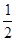 ,那么可求∠B=30°,利用圆周角定理可求∠AOC=60°,而OA=OB,那么△AOC是等边三角形,从而有∠OAC=60°,易求∠OAD=90°,即AD是⊙O的切线;
,那么可求∠B=30°,利用圆周角定理可求∠AOC=60°,而OA=OB,那么△AOC是等边三角形,从而有∠OAC=60°,易求∠OAD=90°,即AD是⊙O的切线;
(2)由于OC⊥AB,OC是半径,利用垂径定理可知OC是AB的垂直平分线,那么CA=CB,而∠B=30°,则∠BAC=30°,于是有∠DAE=60°,∠D=30°,在Rt△ACE中,利用三角函数值可求AE,在Rt△ADE中利用30°的锐角所对的直角边等于斜边的一半,可求AD.
查看习题详情和答案>>
在解直角三角形的过程中,一般要用的主要关系如下(如图所示):在Rt△ABC中,∠C=90°,AC=b,BC=a,AB=c,第1题图
①三边之间的等量关系:( );
②两锐角之间的关系:( );
③边与角之间的关系:
 =( )
=( )  ( )
( )
 ( )
( )  ( )
( )
④直角三角形中成比例的线段(如图所示)。
在Rt△ABC中,∠C=90°,CD⊥AB于D.CD2=( );
AC2=( );BC2=( );AC·BC=( )。
⑤直角三角形的主要线段(如图所示)。
直角三角形斜边上的中线等于斜边的( ),斜边的中点是( )。若r是Rt△ABC(∠C=90°)的内切圆半径,则r=( )=( )。
⑥直角三角形的面积公式.在Rt△ABC中,∠C=90°,S△ABC=( )。(答案不唯一)
①三边之间的等量关系:( );
②两锐角之间的关系:( );
③边与角之间的关系:
 =( )
=( )  ( )
( ) ( )
( )  ( )
( )④直角三角形中成比例的线段(如图所示)。
在Rt△ABC中,∠C=90°,CD⊥AB于D.CD2=( );
AC2=( );BC2=( );AC·BC=( )。
⑤直角三角形的主要线段(如图所示)。
直角三角形斜边上的中线等于斜边的( ),斜边的中点是( )。若r是Rt△ABC(∠C=90°)的内切圆半径,则r=( )=( )。
⑥直角三角形的面积公式.在Rt△ABC中,∠C=90°,S△ABC=( )。(答案不唯一)



第1题图 第④小题图 第⑤小题图