摘要:3.在矩形ABCD中..(>).且.是方程的两个根.P是BC上的一动点.动点Q在PC或其延长线上.BP=PQ.以PQ为一边的正方形为PQRS.点P从B点以/秒的速度开始沿射线BC方向运动.设运动时间为.正方形PQRS与矩形ABCD重叠部分的面积为. (1)求和, (2)分别求出0≤≤2和2≤≤4时 .与之间的函数关系式, (3)是否存在某一时刻.使重叠部分的面积是矩形ABCD面积的.若存在.请求出的值,若不存在.请说明理由. 答案:(1)=4.=2,(2)当0≤≤2时.,当2≤≤4时 .=, (3)当时.取,当==3时., 王江泾镇中学供稿 选择题: 已知抛物线与轴交于A.B两点.顶点为C.连结AC.BC.点A1.A2.A3.-把AC 等分.过各分点作轴的平行线.分别交BC于B1.B2.B3.-.线段A1B1.A2B2.A3B3.-.的和为. A. 2 B. C. D. 填空题: 如图:斜边长为10的直角三角形△ABC中∠C=90°.有一个角∠B=30°.将直角三角形ABC绕着点A逆时针旋转成如图所示.使点F.A.C成一直线.再沿AC方向平移△AEF.使E点落在BC边上.则三角形AEF移动的距离为 解答题: 嘉兴历来被称为“鱼米之乡.丝绸之府 .特别是在建设社会主义新农村的今天.嘉兴的丝织业蓬勃发展.欣欣向荣.但同学们知道吗.在这里有我们的数学知识在默默地奉献.如图是高科技工业--喷气织机的一个自动装置.它有两部分组成:两条对称的抛物线型合成的活动底座和可以绕着底座中心O自由转动的有弹性的直轴AB.当直轴转动时.端点(A.B)也相应紧贴着底座运动.经测量.两抛物线的交接点M.N间的距离是10厘米.两顶点(P.Q)间的距离为50厘米. (1) 若以O点为原点.直线MN为横轴作直角坐标系.求这两条抛物线的解析式.并写出相应的自变量取值范围, (2) 当AB转动时(不与MN重合).求证:四边形AMBN始终是平行四边形, (3) 当AB转动时(不与MN重合).平行四边形AMBN的面积有没有最大值和最小值.若存在.求出点A的坐标.并判断它是何种特殊平行四边形.求出它的面积,若不存在.请说明理由. 油车港镇中学初三备课组供稿
网址:http://m.1010jiajiao.com/timu3_id_449130[举报]
如图,在矩形ABCD中,对角线AC的长为10,且AB、BC(AB>BC)的长是关于x的方程x2+2(1-m)x+6m=0的两个根.
(1)求m的值;
(2)若E是AB上的一点,CF⊥DE于F,求BE为何值时,△CEF的面积是△CED的面积的
,请说明理由.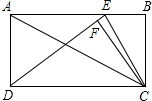 查看习题详情和答案>>
查看习题详情和答案>>
(1)求m的值;
(2)若E是AB上的一点,CF⊥DE于F,求BE为何值时,△CEF的面积是△CED的面积的
| 1 | 3 |
 查看习题详情和答案>>
查看习题详情和答案>>
如图,在矩形ABCD中,对角线AC的长为10,且AB、BC(AB>BC)的长是关于x的方程x2+2(1-m)x+6m=0的两个根.
(1)求m的值;
(2)若E是AB上的一点,CF⊥DE于F,求BE为何值时,△CEF的面积是△CED的面积的 ,请说明理由.
,请说明理由.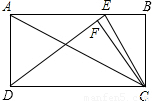
查看习题详情和答案>>
(1)求m的值;
(2)若E是AB上的一点,CF⊥DE于F,求BE为何值时,△CEF的面积是△CED的面积的
 ,请说明理由.
,请说明理由.
查看习题详情和答案>>
如图,在矩形ABCD中,BC=acm,AB=bcm,a>b,且a、b是方程
+
=1的两个根.P是BC上一动点,动点Q在PC或其延长线上,BP=PQ,以PQ为一边的正方形为PQRS.点P从B点开始沿射线BC方向运动,设BP=xcm,正方形PQRS与矩形ABCD重叠部分的面积为ycm2.
(1)求a和b;
(2)分别求出0≤x≤2和2≤x≤4,y与x之间的函数关系式;
(3)在同一坐标系内画出(2)中函数的图象.
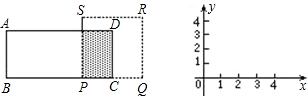 查看习题详情和答案>>
查看习题详情和答案>>
| 8-4x |
| x(x+5) |
| 2x+3 |
| x+5 |
(1)求a和b;
(2)分别求出0≤x≤2和2≤x≤4,y与x之间的函数关系式;
(3)在同一坐标系内画出(2)中函数的图象.
 查看习题详情和答案>>
查看习题详情和答案>>
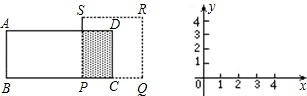
如图,在矩形ABCD中,BC=acm,AB=bcm,a>b,且a、b是方程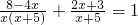 的两个根.P是BC上一动点,动点Q在PC或其延长线上,BP=PQ,以PQ为一边的正方形为PQRS.点P从B点开始沿射线BC方向运动,设BP=xcm,正方形PQRS与矩形ABCD重叠部分的面积为ycm2.
的两个根.P是BC上一动点,动点Q在PC或其延长线上,BP=PQ,以PQ为一边的正方形为PQRS.点P从B点开始沿射线BC方向运动,设BP=xcm,正方形PQRS与矩形ABCD重叠部分的面积为ycm2.
(1)求a和b;
(2)分别求出0≤x≤2和2≤x≤4,y与x之间的函数关系式;
(3)在同一坐标系内画出(2)中函数的图象.
查看习题详情和答案>>
如图,在矩形ABCD中,已知边AB、BC的长恰为关于x的一元二次方程x2-(m-2)x+3m=0的两根.动点P、Q分别从点B、C出发,其中,点P以每秒a个单位的速度,沿B→C的路线向点C运动;点Q以每秒3个单位的速度,沿C→D的路线向点D运动.若P、Q两点同时出发,运动时间为t(s)(t>0),且当t=2时,P、Q两点恰好同时到达目的地.
(1)求m、a的值;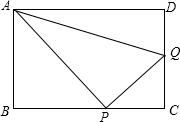
(2)是否存在这样的t,使得△APQ为直角三角形?若存在,请求出所有符合条件的t的值;若不存在,请说明理由.
(3)若在动点P、Q从起点出发的同时,另有M、N两点同时从点A出发,其中,点M以每秒2个单位的速度,沿A→D的路线向点D运动;点N以每秒1个单位的速度,沿A→B的路线向点B运动.问:是否存在这样的t,使得四边形PQMN为平行四边形?若存在,请求出所有符合条件的t的值;若不存在,请说明理由.若将“平行四边形”改为“梯形”,结果又如何? 查看习题详情和答案>>
(1)求m、a的值;

(2)是否存在这样的t,使得△APQ为直角三角形?若存在,请求出所有符合条件的t的值;若不存在,请说明理由.
(3)若在动点P、Q从起点出发的同时,另有M、N两点同时从点A出发,其中,点M以每秒2个单位的速度,沿A→D的路线向点D运动;点N以每秒1个单位的速度,沿A→B的路线向点B运动.问:是否存在这样的t,使得四边形PQMN为平行四边形?若存在,请求出所有符合条件的t的值;若不存在,请说明理由.若将“平行四边形”改为“梯形”,结果又如何? 查看习题详情和答案>>