摘要：l 行程问题: 1) 追及问题:a.两个物体在同一地点不同时间同向出发最后在同一地点的行程问题 等量关系:甲路程=乙路程 甲速度×甲时间=乙速度× b.两个物体从不同地点同时同向出发最后在同一地点的行程问题 等量关系:甲路程-乙路程=原相距路程 2) 相遇问题:两个物体同时从不同地点出发相向而行最后相遇的行程问题 等量关系:甲路程+乙路程=相遇路程 甲速度×相遇时间+乙速度×相遇时间=原两地的路程 3) 一般行程问题: 等量关系:速度×时间=路程 4) 航行问题: 等量关系:顺水速度=静水速度+水流速度 逆水速度=静水速度-水流速度 练习:1.一队学生去校外进行军事野营训练.他们以5千米/时的速度行进.走了18分钟的时候.学校要将一个紧急通知传给队长.通讯员骑自行车以14千米/时的速度按原路追上去.通讯员用多少时间可以追上学生队伍?
网址：http://m.1010jiajiao.com/timu3_id_448239[举报]
教材中第25章锐角的三角比，在这章的小结中有如下一段话：锐角三角比定量地描述了在直角三角形中边角之间的联系．在直角三角形中，一个锐角的大小与两条边长的比值相互唯一确定，因此边长与角的大小之间可以相互转化．
类似的，可以在等腰三角形中建立边角之间的联系，我们定义：等腰三角形中底边与腰的比叫做顶角的正对（sad）．如图，在△ABC中，AB=AC，顶角A的正对记作sadA，这时sad A=
=
．容易知道一个角的大小与这个角的正对值也是相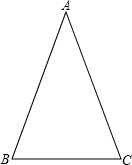
互唯一确定的．
根据上述对角的正对定义，解下列问题：
（1）sad 60°的值为（ B ）
A.
；B.1；C.
；D.2
（2）对于0°＜A＜180°，∠A的正对值sad A的取值范围是 ．
（3）已知sinα=
，其中α为锐角，试求sadα的值．
查看习题详情和答案>>
类似的，可以在等腰三角形中建立边角之间的联系，我们定义：等腰三角形中底边与腰的比叫做顶角的正对（sad）．如图，在△ABC中，AB=AC，顶角A的正对记作sadA，这时sad A=
| 底边 |
| 腰 |
| BC |
| AB |
互唯一确定的．根据上述对角的正对定义，解下列问题：
（1）sad 60°的值为（ B ）
A.
| 1 |
| 2 |
| ||
| 2 |
（2）对于0°＜A＜180°，∠A的正对值sad A的取值范围是
（3）已知sinα=
| 3 |
| 5 |
为了让学生了解文明礼仪知识，增强文明意识，养成文明习惯．某市在“文明校园，从我做起”知识普及活动中，举行了一次“文明礼仪知识”竞赛，共有4000名学生参加了这次竞赛．为了了解本次竞赛的成绩情况，从中抽取75名学生的成绩（得分取正整数，满分为100分）进行了统计．
请你根据上面尚未完成并有局部污损的频数分布表和频数分布直方图，解答下列问题：
（1）求频数分布表中的m、n；
（2）补全频数分布直方图，并画出频数分布折线图（画在原图上）；
（3）所有参加这次竞赛的学生中，得分在80分以上（不包括80分）的学生约有多少名？
查看习题详情和答案>>
请你根据上面尚未完成并有局部污损的频数分布表和频数分布直方图，解答下列问题：
| 组别 | 分组 | 频数 | 频率 |
| 1 | 50.5～60.5 | 6 | 0.08 |
| 2 | 60.5～70.5 | 9 | 0.12 |
| 3 | 70.5～80.5 | 15 | m |
| 4 | 80.5～90.5 | 24 | 0.32 |
| 5 | 90.5～100.5 | n | 0.28 |
| 合计 |
（1）求频数分布表中的m、n；
（2）补全频数分布直方图，并画出频数分布折线图（画在原图上）；
（3）所有参加这次竞赛的学生中，得分在80分以上（不包括80分）的学生约有多少名？