摘要：24．解. (1)OA=OB.DF=EF.DE=AC.AG=DG.EG=CG. ------------3分 (2)ME=GM. 理由是:连EO并延长交⊙O于点N.连结DN. ∵EM是⊙O的切线. ∴∠OEM=90º.∴∠GEM+∠GEN=90º. ----------------5分 ∵EN是⊙O的直径.∠N+∠GEN=90º. ∴∠N=∠GEM. ------------------------7分 ∵AB是⊙O的直径.∴∠B+∠BAC=90º. ∵∠AGF+∠GAF=90º.∴∠AGF=∠B.--------------9分 ∵∠AGF=∠CGE.∴∠CGE=∠B. ∵AC=DE.∴∠N=∠B. ∴∠GEM=∠CGE.∴MG=ME. ------------------11分 (3)答案:.-------------------------14分 28 如图:矩形的顶点在坐标原点O.OA在y轴上.A点坐标为(0.3).另一边OB在x的正半轴上,点M是AC边的中点.点P是OB边上一动点,PF⊥OM.PE⊥BM.垂足分别为E.F． (1)若四边形PEMF为矩形.求B点坐标, 的条件下.求过A.M.B三点的抛物线解析式, (3)在抛物线上是否存在一点N.使得四边形AMON是平行四边形.若存在.求出点N的坐标.若不存在.说明理由.
网址：http://m.1010jiajiao.com/timu3_id_448131[举报]
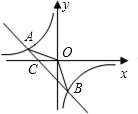如图已知A（-4，n），B（2，-4）是一次函数y=kx+b的图象和反比例函数y=| m |
| x |
（1）求反比例函数和一次函数的解析式；
（2）求直线AB与x轴的交点C的坐标及△AOB的面积；
（3）求不等式kx+b-
| m |
| x |
（4）试说明OA=OB．
如图，△AOB中，OA=OB，∠AOB=90゜，AD平分∠OAB交OB于D，OE⊥AD交AB于E，垂足为F，如图1，两个不全等的等腰直角三角形OAB和OCD叠放在一起，并且有公共的直角顶点O．
（1）在图1中，你发现线段AC，BD的数量关系是
（2）将图1中的△OAB绕点O顺时针旋转90°角，这时（1）中的两个结论是否成立？请做出判断并说明理由．
（3）将图1中的△OAB绕点O顺时针旋转一个锐角，得到图3，这时（1）中的两个结论是否成立？请作出判断并说明理由．
解：（2）在图2中，（1）中的两个结论
理由如下：延长CA交BD于点
（2）在图3中，（1）中的两个结论
理由如下：延长CA交BD于点
查看习题详情和答案>>
（1）在图1中，你发现线段AC，BD的数量关系是
相等
相等
，直线AC，BD相交成90
90
度角．（2）将图1中的△OAB绕点O顺时针旋转90°角，这时（1）中的两个结论是否成立？请做出判断并说明理由．
（3）将图1中的△OAB绕点O顺时针旋转一个锐角，得到图3，这时（1）中的两个结论是否成立？请作出判断并说明理由．
解：（2）在图2中，（1）中的两个结论
成立
成立
（是否成立）；理由如下：延长CA交BD于点
E，∵等腰直角三角形OAB和OCD，
∴OA=OB，OC=OD，
∵AC2=AO2+CO2，BD2=OD2+OB2，
∴AC=BD；
∴△DOB≌△COA（SSS），
∴∠CAO=∠DBO，∠ACO=∠BDO，
∵∠ACO+∠CAO=90°，
∴∠ACO+∠DBO=90°，则∠AEB=90°，即直线AC，BD相交成90°角．
∴OA=OB，OC=OD，
∵AC2=AO2+CO2，BD2=OD2+OB2，
∴AC=BD；
∴△DOB≌△COA（SSS），
∴∠CAO=∠DBO，∠ACO=∠BDO，
∵∠ACO+∠CAO=90°，
∴∠ACO+∠DBO=90°，则∠AEB=90°，即直线AC，BD相交成90°角．
E，∵等腰直角三角形OAB和OCD，
∴OA=OB，OC=OD，
∵AC2=AO2+CO2，BD2=OD2+OB2，
∴AC=BD；
∴△DOB≌△COA（SSS），
∴∠CAO=∠DBO，∠ACO=∠BDO，
∵∠ACO+∠CAO=90°，
∴∠ACO+∠DBO=90°，则∠AEB=90°，即直线AC，BD相交成90°角．
；∴OA=OB，OC=OD，
∵AC2=AO2+CO2，BD2=OD2+OB2，
∴AC=BD；
∴△DOB≌△COA（SSS），
∴∠CAO=∠DBO，∠ACO=∠BDO，
∵∠ACO+∠CAO=90°，
∴∠ACO+∠DBO=90°，则∠AEB=90°，即直线AC，BD相交成90°角．
（2）在图3中，（1）中的两个结论
成立
成立
（是否成立）；理由如下：延长CA交BD于点
F
F
，交OD于点E
E
．问题解决：
（1）在某地有一个山洞，里面藏着无数的财宝，在山洞的入口处有8块标牌，上面有如下数学算式：
经人破解，发现原来在上述的某个数学算式后面有一个开启山洞大门的金钥匙，其它的什么都没有．你只能计算一次拿到钥匙，里面的所有财宝就都是你的：假如你没有拿到钥匙，那么所有的财宝你都拿不到了．把上述算式进行计算后，钥匙就在绝对值最小的标牌下面，聪明的你能拿到所有的财宝吗？试试看！
（2）小明在做数学作业时，不小心打翻了墨水，把一道解方程
(2+?x）+1=x题污染了，小明灵机一动，翻看了书后的参考答案，知道这个方程的解x=-2.5，于是他很快确定了被污染的“?”部分，复原出原方程，你能知道小明是如何求出被污染部分的？
（3）如图，OA⊥OB，OC⊥OD，∠BOC=28°，求∠AOD的度数．
查看习题详情和答案>>
（1）在某地有一个山洞，里面藏着无数的财宝，在山洞的入口处有8块标牌，上面有如下数学算式：
经人破解，发现原来在上述的某个数学算式后面有一个开启山洞大门的金钥匙，其它的什么都没有．你只能计算一次拿到钥匙，里面的所有财宝就都是你的：假如你没有拿到钥匙，那么所有的财宝你都拿不到了．把上述算式进行计算后，钥匙就在绝对值最小的标牌下面，聪明的你能拿到所有的财宝吗？试试看！
（2）小明在做数学作业时，不小心打翻了墨水，把一道解方程
| 1 | 3 |
（3）如图，OA⊥OB，OC⊥OD，∠BOC=28°，求∠AOD的度数．
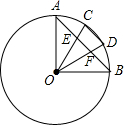如图，在⊙O中，半径OA⊥OB，C、D为弧AB的三等分点．弦AB分别交OC、OD于点E、F，下列结论：①∠AOC=30°；②CE=DF；③∠AEO=105°；④AE=EF=FB．其中正确的有