题目内容
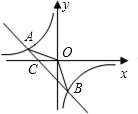 如图已知A(-4,n),B(2,-4)是一次函数y=kx+b的图象和反比例函数y=
如图已知A(-4,n),B(2,-4)是一次函数y=kx+b的图象和反比例函数y=| m |
| x |
(1)求反比例函数和一次函数的解析式;
(2)求直线AB与x轴的交点C的坐标及△AOB的面积;
(3)求不等式kx+b-
| m |
| x |
(4)试说明OA=OB.
分析:(1)把A(-4,n),B(2,-4)分别代入一次函数y=kx+b和反比例函数y=
,运用待定系数法分别求其解析式;
(2)把三角形AOB的面积看成是三角形AOC和三角形OCB的面积之和进行计算.
(3)根据图象可以得出:不等式kx+b-
<0的解集为:kx+b<
的解集,结合A,B两点横坐标得出;
(4)根据A(-4,2),B(2,-4),得出AO,BO的长即可得出答案.
| m |
| x |
(2)把三角形AOB的面积看成是三角形AOC和三角形OCB的面积之和进行计算.
(3)根据图象可以得出:不等式kx+b-
| m |
| x |
| m |
| x |
(4)根据A(-4,2),B(2,-4),得出AO,BO的长即可得出答案.
解答:解:(1)∵B(2,-4)在y=
上,
∴m=-8.
∴反比例函数的解析式为y=-
.
∵点A(-4,n)在y=-
上,
∴n=2.
∴A(-4,2).
∵y=kx+b经过A(-4,2),B(2,-4),
∴
.
解得:
,
∴一次函数的解析式为y=-x-2.
(2)∵C是直线AB与x轴的交点,
∴当y=0时,x=-2.
∴点C(-2,0).
∴OC=2.
∴S△AOB=S△ACO+S△BCO=
×2×2+
×2×4=6.
(3)根据图象可以得出:不等式kx+b-
<0的解集为:kx+b<
的解集,结合A,B两点横坐标得出:
即-4<x<0,或x>2时;不等式kx+b-
<0;
(4)∵A(-4,2),B(2,-4),
∴AO=
=2
,BO=
=2
,
∴AO=BO.
| m |
| x |
∴m=-8.
∴反比例函数的解析式为y=-
| 8 |
| x |
∵点A(-4,n)在y=-
| 8 |
| x |
∴n=2.
∴A(-4,2).
∵y=kx+b经过A(-4,2),B(2,-4),
∴
|
解得:
|

∴一次函数的解析式为y=-x-2.
(2)∵C是直线AB与x轴的交点,
∴当y=0时,x=-2.
∴点C(-2,0).
∴OC=2.
∴S△AOB=S△ACO+S△BCO=
| 1 |
| 2 |
| 1 |
| 2 |
(3)根据图象可以得出:不等式kx+b-
| m |
| x |
| m |
| x |
即-4<x<0,或x>2时;不等式kx+b-
| m |
| x |
(4)∵A(-4,2),B(2,-4),
∴AO=
| 42+22 |
| 5 |
| 42+22 |
| 5 |
∴AO=BO.
点评:本题考查了用待定系数法确定反比例函数的比例系数k,求出函数解析式以及利用图象得出不等式解集;要能够熟练借助直线和y轴的交点运用分割法求得不规则图形的面积是解题关键.

练习册系列答案
相关题目
 8、如图已知D是△ABC的边BC的中点,过D作两条互相垂直的射线,分别交AB于E,交AC于F,求证:BE+CF>EF.
8、如图已知D是△ABC的边BC的中点,过D作两条互相垂直的射线,分别交AB于E,交AC于F,求证:BE+CF>EF.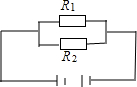 如图已知电阻R1,R2并联在电路中,且R1+R2=10Ω,请用所学过的数学知识讨论一下R1,R2分别为多少时,该电路的总电阻最大,最大电阻是多少?
如图已知电阻R1,R2并联在电路中,且R1+R2=10Ω,请用所学过的数学知识讨论一下R1,R2分别为多少时,该电路的总电阻最大,最大电阻是多少?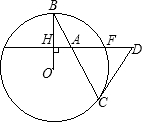 如图已知OB是半径,弦EF垂直OB于H,点A是HF上的一点,BA和⊙O相交于另一点C,过点C的切线和EF的延长线交于点D:
如图已知OB是半径,弦EF垂直OB于H,点A是HF上的一点,BA和⊙O相交于另一点C,过点C的切线和EF的延长线交于点D: 10、如图已知∠ACB=90°,CD⊥AB于D,则图中表示点到直线的距离的线段的条数是( )
10、如图已知∠ACB=90°,CD⊥AB于D,则图中表示点到直线的距离的线段的条数是( ) 如图已知AB∥EF,∠BED=∠B+∠D,求证:AB∥CD
如图已知AB∥EF,∠BED=∠B+∠D,求证:AB∥CD