摘要：23． 如图16.在平面直角坐标系中.矩形ABCO的面积为15.边OA比OC大2．E为BC的中点.以OE为直径的⊙O′交轴于D点.过点D作DF⊥AE于点F． (1) 求OA.OC的长, (2) 求证:DF为⊙O′的切线, (3) 小明在解答本题时.发现△AOE是等腰三角形．由此.他断定:“直线BC上一定存在除点E以外的点P.使△AOP也是等腰三角形.且点P一定在⊙O′外 ．你同意他的看法吗?请充分说明理由． 解:
网址：http://m.1010jiajiao.com/timu3_id_448123[举报]
如图16，在平面直角坐标系中，直线
与
轴交于点
，与
轴交于点
，抛物线
经过
三点．
（1）求过三点抛物线的解析式并求出顶点
的坐标；
（2）在抛物线上是否存在点
，使
为直角三角形，若存在，直接写出点坐标；若不存在，请说明理由；
（3）试探究在直线
上是否存在一点
，使得
的周长最小，若存在，求出点的坐标；若不存在，请说明理由．
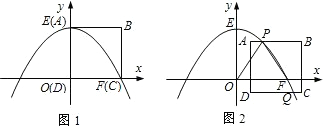如图1，在平面直角坐标系中，抛物线y=ax2+c与x轴正半轴交于点F（16，0），与y轴正半轴交于点E（0，16），边长为16的正方形ABCD的顶点D与原点O重合，顶点A与点E重合，顶点C与点F重合．（1）求抛物线的函数表达式；
（2）如图2，若正方形ABCD在平面内运动，并且边BC所在的直线始终与x轴垂直，抛物线始终与边AB交于点P且同时与边CD交于点Q（运动时，点P不与A，B两点重合，点Q不与C，D两点重合）．设点A的坐标为（m，n）（m＞0）．
①当PO=PF时，分别求出点P和点Q的坐标；
②在①的基础上，当正方形ABCD左右平移时，请直接写出m的取值范围；
③当n=7时，是否存在m的值使点P为AB边的中点？若存在，请求出m的值；若不存在，请说明理由． 查看习题详情和答案>>
如图1，在平面直角坐标系中，点A（4，4），点B、C分别在x轴、y轴的正半轴上，S四边形OBAC=16．
（1）∠COA的值为
（2）求∠CAB的度数；
（3）如图2，点M、N分别是x轴正半轴及射线OA上一点，且OH⊥MN的延长线于H，满足∠HON=∠NMO，请探究两条线段MN、OH之间的数量关系，并给出证明．
查看习题详情和答案>>
（1）∠COA的值为
45°
45°
；（2）求∠CAB的度数；
（3）如图2，点M、N分别是x轴正半轴及射线OA上一点，且OH⊥MN的延长线于H，满足∠HON=∠NMO，请探究两条线段MN、OH之间的数量关系，并给出证明．
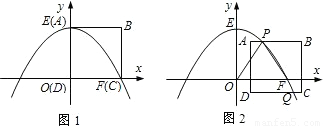
如图1，在平面直角坐标系中，抛物线y=ax2+c与x轴正半轴交于点F（16，0），与y轴正半轴交于点E（0，16），边长为16的正方形ABCD的顶点D与原点O重合，顶点A与点E重合，顶点C与点F重合．
（1）求抛物线的函数表达式；
（2）如图2，若正方形ABCD在平面内运动，并且边BC所在的直线始终与x轴垂直，抛物线始终与边AB交于点P且同时与边CD交于点Q（运动时，点P不与A，B两点重合，点Q不与C，D两点重合）．设点A的坐标为（m，n）（m＞0）．
①当PO=PF时，分别求出点P和点Q的坐标；
②在①的基础上，当正方形ABCD左右平移时，请直接写出m的取值范围；
③当n=7时，是否存在m的值使点P为AB边的中点？若存在，请求出m的值；若不存在，请说明理由．
查看习题详情和答案>>
（1）求抛物线的函数表达式；
（2）如图2，若正方形ABCD在平面内运动，并且边BC所在的直线始终与x轴垂直，抛物线始终与边AB交于点P且同时与边CD交于点Q（运动时，点P不与A，B两点重合，点Q不与C，D两点重合）．设点A的坐标为（m，n）（m＞0）．
①当PO=PF时，分别求出点P和点Q的坐标；
②在①的基础上，当正方形ABCD左右平移时，请直接写出m的取值范围；
③当n=7时，是否存在m的值使点P为AB边的中点？若存在，请求出m的值；若不存在，请说明理由．
查看习题详情和答案>>
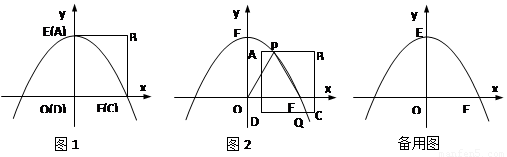
如图1，在平面直角坐标系中，拋物线y=ax2+c与x轴正半轴交于点F(16，0)、与y轴正半轴交于点E(0，16)，边长为16的正方形ABCD的顶点D与原点O重合，顶点A与点E重合，顶点C与点F重合；
1.求拋物线的函数表达式
2.如图2，若正方形ABCD在平面内运动，并且边BC所在的直线始终与x轴垂直，抛物线始终与边AB交于点P且同时与边CD交于点Q(运动时，点P不与A、B两点重合，点Q不与C、D两点重合)。设点A的坐标为(m，n) (m>0)。
j 当PO=PF时，分别求出点P和点Q的坐标；
k 在j的基础上，当正方形ABCD左右平移时，请直接写出m的取值范围；
l 当n=7时，是否存在m的值使点P为AB边中点。若存在，请求出m的值；若不存在，请说明理由。
查看习题详情和答案>>