题目内容
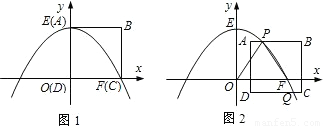
如图16,在平面直角坐标系中,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,抛物线
,抛物线![]() 经过
经过![]() 三点.
三点.
(1)求过![]() 三点抛物线的解析式并求出顶点
三点抛物线的解析式并求出顶点![]() 的坐标;
的坐标;
(2)在抛物线上是否存在点![]() ,使
,使![]() 为直角三角形,若存在,直接写出
为直角三角形,若存在,直接写出![]() 点坐标;若不存在,请说明理由;
点坐标;若不存在,请说明理由;
(3)试探究在直线![]() 上是否存在一点
上是否存在一点![]() ,使得
,使得![]() 的周长最小,若存在,求出
的周长最小,若存在,求出![]() 点的坐标;若不存在,请说明理由.
点的坐标;若不存在,请说明理由.

解:(1)![]() 直线
直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() .
.
![]() ,
,![]() ························································································· 1分
························································································· 1分
![]() 点
点![]() 都在抛物线上,
都在抛物线上,
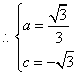
![]() 抛物线的解析式为
抛物线的解析式为![]() ························································ 3分
························································ 3分
![]() 顶点
顶点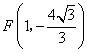 ······························································································· 4分
······························································································· 4分
(2)存在··············································································································· 5分
![]() ············································································································· 7分
············································································································· 7分
![]() ············································································································ 9分
············································································································ 9分
(3)存在·············································································································· 10分
理由:
解法一:
延长![]() 到点
到点![]() ,使
,使![]() ,连接
,连接![]() 交直线
交直线![]() 于点
于点![]() ,则点
,则点![]() 就是所求的点.
就是所求的点.
····················································································· 11分
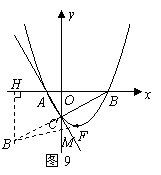 过点
过点![]() 作
作![]() 于点
于点![]() .
.
![]() 点在抛物线
点在抛物线![]() 上,
上,![]()
在![]() 中,
中,![]() ,
,
![]() ,
,![]() ,
,
在![]() 中,
中,![]() ,
,
![]() ,
,![]() ,
,![]() ··············································· 12分
··············································· 12分
设直线![]() 的解析式为
的解析式为![]()
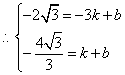 解得
解得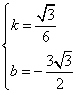
![]() ································································································ 13分
································································································ 13分
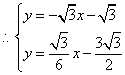 解得
解得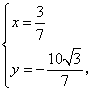
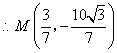
![]() 在直线
在直线![]() 上存在点
上存在点![]() ,使得
,使得![]() 的周长最小,此时
的周长最小,此时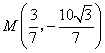 .··· 14分
.··· 14分

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案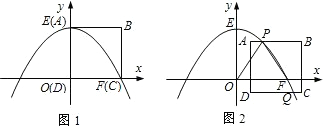 如图1,在平面直角坐标系中,抛物线y=ax2+c与x轴正半轴交于点F(16,0),与y轴正半轴交于点E(0,16),边长为16的正方形ABCD的顶点D与原点O重合,顶点A与点E重合,顶点C与点F重合.
如图1,在平面直角坐标系中,抛物线y=ax2+c与x轴正半轴交于点F(16,0),与y轴正半轴交于点E(0,16),边长为16的正方形ABCD的顶点D与原点O重合,顶点A与点E重合,顶点C与点F重合.