摘要：27．如图1.正方形ABCD的顶点A.B的坐标分别为A.B(8.4).顶点C.D在第一象限.点P从点A出发.沿正方形按逆时针方向匀速运动.同时.点Q从点E(4.0)出发.沿x轴正方向以相同的速度匀速运动.当点P到达点C时.P.Q两点同时停止运动.设运动的时间为t秒. (1)求正方形的边长, (2)当点P在AB边上运动时.△OPQ的面积S与时间t(秒)之间的函数图象为抛物线的一部分.求P.Q两点的运动速度, 中面积S与时间t(秒)的函数关系式及面积S取最大值时点P的坐标. (4)若点P.Q保持(2)中的速度不变.则点P沿着AB边运动时.∠OPQ的大小随着时间t的增大而增大,沿着BC边运动时.∠OPQ的大小随着时间t的增大而减小.当点P沿着这两边运动时.使∠OPQ＝90°的点P有几个? 中考模拟七答案
网址：http://m.1010jiajiao.com/timu3_id_447926[举报]
(本题满分14分)
小题1:(1) 如图所示的网格坐标系中，顶点在格点上的矩形ABCD被分割成四块全等的小矩形①、②、③、④，并经过一次或二次变换拼成正方形A1B1C1D1．试写出小矩形从①→⑤、③→⑦一种变换过程；
小题2:(2) 对任意一个矩形按(1)的方式实施分割、变换后拼成正方形．试探究矩形ABCD的周长与面积分别与正方形A1B1C1D1的周长与面积的大小关系？并用代数方法验证你的结论．
小题1:(1) 如图所示的网格坐标系中，顶点在格点上的矩形ABCD被分割成四块全等的小矩形①、②、③、④，并经过一次或二次变换拼成正方形A1B1C1D1．试写出小矩形从①→⑤、③→⑦一种变换过程；
小题2:(2) 对任意一个矩形按(1)的方式实施分割、变换后拼成正方形．试探究矩形ABCD的周长与面积分别与正方形A1B1C1D1的周长与面积的大小关系？并用代数方法验证你的结论．
(本题满分14分)
【小题1】(1) 如图所示的网格坐标系中，顶点在格点上的矩形ABCD被分割成四块全等的小矩形①、②、③、④，并经过一次或二次变换拼成正方形A1B1C1D1．试写出小矩形从①→⑤、③→⑦一种变换过程；
【小题2】(2) 对任意一个矩形按(1)的方式实施分割、变换后拼成正方形．试探究矩形ABCD的周长与面积分别与正方形A1B1C1D1的周长与面积的大小关系？并用代数方法验证你的结论．
（本题10分） 以四边形ABCD的边AB、BC、CD、DA为斜边分别向外侧作等腰直角三角形，直角顶点分别为E、F、G、H，顺次连结这四个点得四边形EFGH．如图1，当四边形ABCD为正方形时，我们发现四边形EFGH是正方形；
【小题1】（1）如图2，当四边形ABCD为矩形时，则四边形EFGH的形状是 ；（1分）
【小题2】（2）如图3，当四边形ABCD为一般平行四边形时，设∠ADC=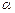
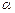（0°＜＜90°），
【小题3】① 试用含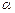的代数式表示∠HAE= ；（1分）
【小题4】② 求证：HE=HG；（4分）③ 四边形EFGH是什么四边形？并说明理由．（4分）
查看习题详情和答案>>
【小题1】（1）如图2，当四边形ABCD为矩形时，则四边形EFGH的形状是 ；（1分）
【小题2】（2）如图3，当四边形ABCD为一般平行四边形时，设∠ADC=
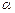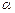（0°＜＜90°），【小题3】① 试用含
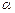的代数式表示∠HAE= ；（1分）【小题4】② 求证：HE=HG；（4分）③ 四边形EFGH是什么四边形？并说明理由．（4分）
查看习题详情和答案>>
（0°＜
