摘要: 如图.边长为1的正方形OABC的顶点A在x轴正半轴上.将正方形OABC绕点O顺时针旋转30°.使点A落在抛物线()图像上.正方形OABC继续顺时针旋转多少度时.点A再次落在抛物线的图像上?并求这个点的坐标. 解:(1)设旋转后点A落在抛物线上点A1处.OA1=1.过A1作A1M⊥x轴 于M.则OM=...由A1在 上得.解得 ∴ (2)由抛物线关于y轴对称.再次旋转后A落在抛物线上的点A2处.点A2与点A1关于y轴对称.易见继续旋转120°.点A2的坐标为
网址:http://m.1010jiajiao.com/timu3_id_447870[举报]
 如图,边长为6的正方OABC的顶点O在坐标原点处,点A、C分别在x轴、y轴的正半轴上,点E是OA边上的点(不与点A重合),EF⊥CE,且与正方形外角平分线AC交于点P.
如图,边长为6的正方OABC的顶点O在坐标原点处,点A、C分别在x轴、y轴的正半轴上,点E是OA边上的点(不与点A重合),EF⊥CE,且与正方形外角平分线AC交于点P.(1)当点E坐标为(3,0)时,证明CE=EP;
(2)如果将上述条件“点E坐标为(3,0)”改为“点E坐标为(t,0)”,结论CE=EP是否仍然成立,请说明理由;
(3)在y轴上是否存在点M,使得四边形BMEP是平行四边形?若存在,用t表示点M的坐标;若不存在,说明理由.
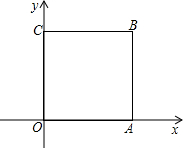
 如图,边长为1的正方形OABC的顶点A、C在坐标轴上,顶点O与原点重合,顶点B在第一象限,则该正方形绕点O逆时针旋转45°后,B点的坐标为
如图,边长为1的正方形OABC的顶点A、C在坐标轴上,顶点O与原点重合,顶点B在第一象限,则该正方形绕点O逆时针旋转45°后,B点的坐标为 如图,边长为6的正方OABC的顶点O在坐标原点处,点A、C分别在x轴、y轴的正半轴上,点E是OA边上的点(不与点A重合),EF⊥CE,且与正方形外角平分线AC交于点P.
如图,边长为6的正方OABC的顶点O在坐标原点处,点A、C分别在x轴、y轴的正半轴上,点E是OA边上的点(不与点A重合),EF⊥CE,且与正方形外角平分线AC交于点P.