题目内容
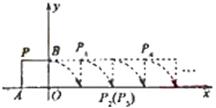
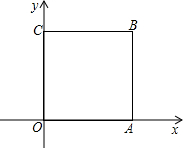如图，边长为1的正方形OABC的顶点A、C在坐标轴上，顶点O与原点重合，顶点B在第一象限，则该正方形绕点O逆时针旋转45°后，B点的坐标为分析：连接OB，边长为1的正方形OABC中，∠BOC=45°，该正方形绕点O逆时针旋转45°后，点B在y轴正半轴上，横坐标为0，纵坐标即为OB的长，利用勾股定理，即可得出；
解答：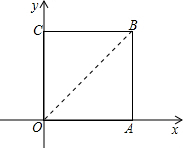
解：如图，连接OB，
∵四边形OABC是正方形，边长为1，
∴∠BOC=45°，OB=
，
∵该正方形绕点O逆时针旋转45°，
∴点B在y轴的正半轴上，
∴横坐标为0，纵坐标即为OB的长，
∴B点的坐标为（0，
）．
故答案为：（0，
）．
解：如图，连接OB，∵四边形OABC是正方形，边长为1，
∴∠BOC=45°，OB=
| 2 |
∵该正方形绕点O逆时针旋转45°，
∴点B在y轴的正半轴上，
∴横坐标为0，纵坐标即为OB的长，
∴B点的坐标为（0，
| 2 |
故答案为：（0，
| 2 |
点评：本题主要考查了坐标与图形变化-旋转，注意：图形旋转之后要结合旋转的角度和图形的特殊性质来求出旋转后的点的坐标．
练习册系列答案
春雨教育同步作文系列答案
相关题目
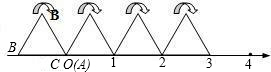
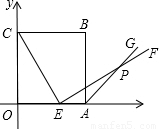
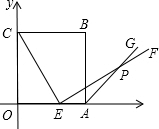如图，边长为6的正方OABC的顶点O在坐标原点处，点A、C分别在x轴、y轴的正半轴上，点E是OA边上的点（不与点A重合），EF⊥CE，且与正方形外角平分线AC交于点P．
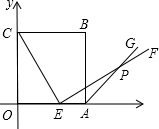如图，边长为6的正方OABC的顶点O在坐标原点处，点A、C分别在x轴、y轴的正半轴上，点E是OA边上的点（不与点A重合），EF⊥CE，且与正方形外角平分线AC交于点P．
轴正方向连续翻转2006次，点P依次落在点
，
，
，
，……
的位置，则
＝_________．
